Question

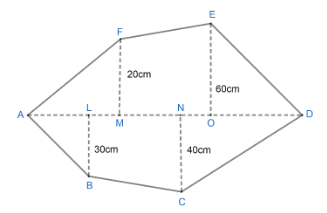
Find the area of the following polygon if $ AL=10cm,AM=20cm. $ $ AN=50cm,AO=60cm\ and\ AD=90cm $

A. $ 337.5c{{m}^{2}} $
B. $ 384c{{m}^{2}} $
C. $ 5500c{{m}^{2}} $
D. $ 5050c{{m}^{2}} $

Answer 1

Hint: To solve the question given above, we will make use of the fact that the polygon given in question is made up of a number of triangles and trapezium. Also, the triangles which are making the polygon is right-angled triangle, so we will find the base length of each triangle and then we will apply the formula of area of triangle i.e. $ Area=\dfrac{b\times h}{2} $ where b is the base and h is the height of the triangle. Then, we will calculate the area of trapezium by the help of the formula: $ Area=\left( \dfrac{a+b}{2} \right)d $ , where a and b are lengths of parallel sides and d is distance between them. The sum of all these areas of triangles and trapeziums will be equal to the area of the polygon.

Complete step-by-step answer:
Before we start to find the area of a given polygon, we will make use of the fact that the polygon given in question is made up of a number of triangles and trapeziums. So, the area of given polygon will be equal to the sum of the areas of these triangles and trapeziums. The area of a triangle with base b and height h is given by:
 $ Area=\dfrac{b\times h}{2} $
The area of trapezium with parallel sides length ‘a’ and ‘b’ and having distance ‘d’ between them is given by:
 $ Area=\left( \dfrac{a+b}{2} \right)d $

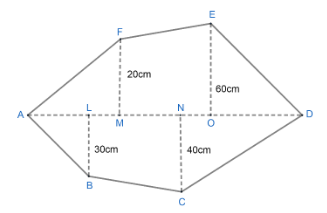
Now, we will calculate the area of $ \Delta AMF $ . The height of $ \Delta AMF $ is MF and base is AM. Thus, we have,
 $ \begin{align}
  & Area\ of\ \Delta AMF=\dfrac{\left( MF \right)\left( AM \right)}{2} \\
 & \Rightarrow Area\ of\ \Delta AMF=\dfrac{20\times 20}{2}c{{m}^{2}} \\
 & \Rightarrow Ar\left( \Delta AMF \right)=\dfrac{400}{2}c{{m}^{2}} \\
 & \Rightarrow Ar\left( \Delta AMF \right)=200c{{m}^{2}}.............\left( 1 \right) \\
\end{align} $
Now, we will calculate the area of $ \Delta ALB $ . The height of $ \Delta ALB $ is LB and base in AL. Thus, we have:
 $ \begin{align}
  & Area\ of\ \left( \Delta ALB \right)=\dfrac{\left( LB \right)\left( AL \right)}{2} \\
 & \Rightarrow Area\ of\ \left( \Delta ALB \right)=\dfrac{30\times 10}{2}c{{m}^{2}} \\
 & \Rightarrow Ar\left( \Delta ALB \right)=150c{{m}^{2}}..................\left( 2 \right) \\
\end{align} $
Now, we will calculate the area of $ \Delta EOD $ . The base is OD and height is EO. Thus, we have,
 $ \begin{align}
  & Ar\ \left( \Delta EOD \right)=\dfrac{\left( OD \right)\left( EO \right)}{2} \\
 & \Rightarrow Ar\ \left( \Delta EOD \right)=\dfrac{\left( AD-AO \right)\left( EO \right)}{2} \\
 & \Rightarrow Ar\ \left( \Delta EOD \right)=\dfrac{\left( 90-60 \right)\left( 60 \right)}{2}c{{m}^{2}} \\
 & \Rightarrow Ar\left( \Delta EOD \right)=30\times 30c{{m}^{2}} \\
 & \Rightarrow Ar\left( \Delta EOD \right)=900c{{m}^{2}}.............\left( 3 \right) \\
\end{align} $
Now, we will calculate the area of $ \Delta CDN $ . The base is ND and height is CN. Thus, we have,
 $ \begin{align}
  & Ar\ \left( \Delta EOD \right)=\dfrac{\left( ND \right)\left( CN \right)}{2} \\
 & \Rightarrow Ar\ \left( \Delta EOD \right)=\dfrac{\left( AD-AN \right)\left( CN \right)}{2} \\
 & \Rightarrow Ar\ \left( \Delta EOD \right)=\dfrac{\left( 90-50 \right)\left( 40 \right)}{2}c{{m}^{2}} \\
 & \Rightarrow Ar\left( \Delta EOD \right)=40\times 20c{{m}^{2}} \\
 & \Rightarrow Ar\left( \Delta EOD \right)=800c{{m}^{2}}.............\left( 4 \right) \\
\end{align} $
Now, we will calculate the area of trapezium EFMO. The parallel sides are MF and OE. The distance between them is OM. Thus, we have:
\[\begin{align}
  & Ar\ \left( trapezium\ EFMO \right)=\dfrac{\left( MF+OE \right)\left( OM \right)}{2} \\
 & \Rightarrow Ar\ \left( trapezium\ EFMO \right)=\dfrac{\left( MF+OE \right)\left( AO-AM \right)}{2} \\
 & \Rightarrow Ar\ \left( trapezium\ EFMO \right)=\dfrac{\left( 20+60 \right)\left( 60-20 \right)}{2}c{{m}^{2}} \\
 & \Rightarrow Ar\ \left( trapezium\ EFMO \right)=\dfrac{80\times 40}{2}c{{m}^{2}} \\
 & \Rightarrow Ar\ \left( trapezium\ EFMO \right)=80\times 20c{{m}^{2}} \\
 & \Rightarrow Ar\ \left( trapezium\ EFMO \right)=1600c{{m}^{2}}.............\left( 5 \right) \\
\end{align}\]
Now, we will calculate the area of trapezium LNCB. The parallel sides are LB and NC. The distance between them is LN. Thus, we have:
\[\begin{align}
  & Ar\ \left( trapezium\ LNCB \right)=\dfrac{\left( LB+NC \right)\left( LN \right)}{2} \\
 & \Rightarrow Ar\ \left( trapezium\ LNCB \right)=\dfrac{\left( LB+NC \right)\left( AN-AL \right)}{2} \\
 & \Rightarrow Ar\ \left( trapezium\ LNCB \right)=\dfrac{\left( 30+40 \right)\left( 50-10 \right)}{2}c{{m}^{2}} \\
 & \Rightarrow Ar\ \left( trapezium\ LNCB \right)=\dfrac{70\times 40}{2}c{{m}^{2}} \\
 & \Rightarrow Ar\ \left( trapezium\ LNCB \right)=1400c{{m}^{2}}.............\left( 6 \right) \\
\end{align}\]
Now, the area of the polygon will be the sum of all the areas of triangles and trapeziums. Thus, we have:
 $ \begin{align}
  & Area\ of\ polygon=Ar\left( \Delta AMF \right)+Ar\left( \Delta ALB \right)+Ar\left( \Delta EOD \right)+Ar\left( \Delta CDN \right) \\
 & +Ar\left( trapezium\ EFMO \right)+Ar\left( trapezium\ LNCB \right) \\
 & \Rightarrow Area\ of\ polygon=200c{{m}^{2}}+150c{{m}^{2}}+900c{{m}^{2}}+800c{{m}^{2}}+1600c{{m}^{2}}+1400c{{m}^{2}} \\
 & \Rightarrow Area\ of\ polygon=5050c{{m}^{2}} \\
\end{align} $
So, the correct answer is “Option D”.

Note: While solving the question, we have assumed that FM, EO, LB and NC are heights or respective triangles. In other words, we have indirectly assumed that FM, EO, LB and NC are perpendicular to line AD. This assumption is necessary to be taken because in our case, the limited information is given in question.