
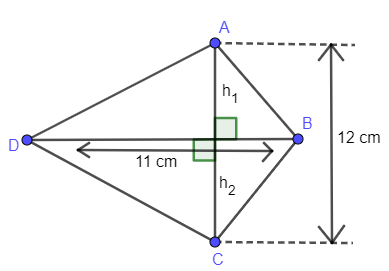
Find the area of quadrilateral ABCD.

Answer
610.8k+ views
Hint:First look at the figure given and try to find out the name of shape. By using different properties you can eliminate some of the shapes and arrive at the conclusion of a particular shape. By using knowledge of geometry try to change the formula or area and use the formula of area and use the formula which is suitable for the given question.
Complete step-by-step answer:
The given quadrilateral
So, you can see the lengths of diagonals are different.
By above you can eliminate squares and rectangles.
You can see diagonals are bisecting. So, you can eliminate kites from this condition.
Now by observation, you can see diagonals are perpendicular to each other. So, we can confirm that it is rhombus by above conditions.
Now take diagonal DB, it is dividing the shape into 2 triangles with the same base BD.
As we know that diagonals bisects each other we say the height of both triangles is half the length of AC.
By above conditions we can say area of ABCD, is:
Area of ABCD $=$ Area of $\Delta ABD+$ Area of $\Delta BCD$
$\Delta ABD=\dfrac{1}{2}\times base\times height$
Above formula is well known from geometry
$\Delta ABD=\Delta BCD=\dfrac{1}{2}\times 11\times 6=33$
Area of ABCD $=2\times 33$
$=66\text{ sq}\text{. cm}$
Note: Alternate method is to apply direct formula that area $=\dfrac{1}{2}\left( {{d}_{1}}{{d}_{2}} \right)$ where ${{d}_{1}},{{d}_{2}}$ are lengths of the diagonals i.e ${{d}_{1}}=12cm$ and ${{d}_{2}}=11cm$ by substituting in above formula we get required answer.Students should remember the formulas of area of triangle and quadrilateral to solve these types of questions.
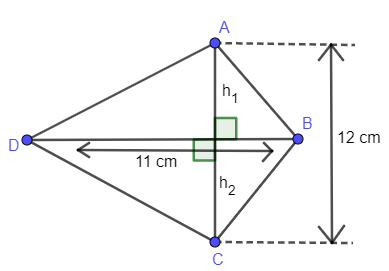
Complete step-by-step answer:
The given quadrilateral

So, you can see the lengths of diagonals are different.
By above you can eliminate squares and rectangles.
You can see diagonals are bisecting. So, you can eliminate kites from this condition.
Now by observation, you can see diagonals are perpendicular to each other. So, we can confirm that it is rhombus by above conditions.
Now take diagonal DB, it is dividing the shape into 2 triangles with the same base BD.
As we know that diagonals bisects each other we say the height of both triangles is half the length of AC.
By above conditions we can say area of ABCD, is:
Area of ABCD $=$ Area of $\Delta ABD+$ Area of $\Delta BCD$
$\Delta ABD=\dfrac{1}{2}\times base\times height$
Above formula is well known from geometry
$\Delta ABD=\Delta BCD=\dfrac{1}{2}\times 11\times 6=33$
Area of ABCD $=2\times 33$
$=66\text{ sq}\text{. cm}$
Note: Alternate method is to apply direct formula that area $=\dfrac{1}{2}\left( {{d}_{1}}{{d}_{2}} \right)$ where ${{d}_{1}},{{d}_{2}}$ are lengths of the diagonals i.e ${{d}_{1}}=12cm$ and ${{d}_{2}}=11cm$ by substituting in above formula we get required answer.Students should remember the formulas of area of triangle and quadrilateral to solve these types of questions.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




