Question

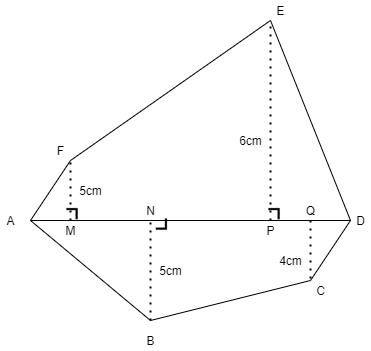
Find the area of polygon ABCDEF, if \[AD=18cm\], \[AQ=14cm\], \[AP=12cm\], \[AN=8cm\],
\[AM=4cm\] and FM, EP, QC and BN are perpendicular to diagonal AD.

Answer 1

Hint: We solve this problem simply by dividing the given figure into parts of triangles and trapeziums and find the areas respectively. Then, we add all the areas to get the required area. We have the area formula of triangle as
\[\text{Area of triangle}=\dfrac{1}{2}\left( base \right)\left( height \right)\]
Also we have the area formula of trapezium as
\[\text{Area of trapezium}=\dfrac{1}{2}\left( \text{distance between parallel sides} \right)\left( \text{sum of parallel sides} \right)\]
By using these two formulas we find the area of the given figure.

Complete step by step answer:
We are given that the lengths of some sides as\[AD=18cm\], \[AQ=14cm\], \[AP=12cm\], \[AN=8cm\],
\[AM=4cm\].
Here, we can see that in the figure we have some parts like triangles and trapeziums.
Let us consider the triangle \[\Delta AFM\].
Let us assume that the area of \[\Delta AFM\]as \[{{A}_{1}}\].
We know that the area formula of triangle is given as
\[\text{Area of triangle}=\dfrac{1}{2}\left( base \right)\left( height \right)\]
By using the above formula to triangle \[\Delta AFM\] we get
\[\Rightarrow {{A}_{1}}=\dfrac{1}{2}\left( AM \right)\left( FM \right)\]
By substituting the required values we get
\[\begin{align}
  & \Rightarrow {{A}_{1}}=\dfrac{1}{2}\left( 4cm \right)\left( 5cm \right) \\
 & \Rightarrow {{A}_{1}}=10c{{m}^{2}} \\
\end{align}\]
Now, let us consider the triangle \[\Delta EPD\].
Let us assume that the area of \[\Delta EPD\]as \[{{A}_{2}}\].
We know that the area formula of triangle is given as
\[\text{Area of triangle}=\dfrac{1}{2}\left( base \right)\left( height \right)\]
By using the above formula to triangle \[\Delta EPD\] we get
\[\Rightarrow {{A}_{2}}=\dfrac{1}{2}\left( PD \right)\left( EP \right)\]
Here, we have
\[\begin{align}
  & \Rightarrow PD=AD-AP \\
 & \Rightarrow PD=18cm-12cm \\
 & \Rightarrow PD=6cm \\
\end{align}\]
By substituting the required values we get
\[\begin{align}
  & \Rightarrow {{A}_{2}}=\dfrac{1}{2}\left( 6cm \right)\left( 6cm \right) \\
 & \Rightarrow {{A}_{2}}=18c{{m}^{2}} \\
\end{align}\]
Now, let us consider the triangle \[\Delta DQC\].
Let us assume that the area of \[\Delta DQC\]as \[{{A}_{3}}\].
We know that the area formula of triangle is given as
\[\text{Area of triangle}=\dfrac{1}{2}\left( base \right)\left( height \right)\]
By using the above formula to triangle \[\Delta DQC\] we get
\[\Rightarrow {{A}_{3}}=\dfrac{1}{2}\left( QD \right)\left( QC \right)\]
Here, we have
\[\begin{align}
  & \Rightarrow QD=AD-AQ \\
 & \Rightarrow QD=18cm-14cm \\
 & \Rightarrow QD=4cm \\
\end{align}\]
By substituting the required values we get
\[\begin{align}
  & \Rightarrow {{A}_{3}}=\dfrac{1}{2}\left( 4cm \right)\left( 6cm \right) \\
 & \Rightarrow {{A}_{3}}=12c{{m}^{2}} \\
\end{align}\]
Now, let us consider the triangle \[\Delta ANB\].
Let us assume that the area of \[\Delta ANB\]as \[{{A}_{4}}\].
We know that the area formula of triangle is given as
\[\text{Area of triangle}=\dfrac{1}{2}\left( base \right)\left( height \right)\]
By using the above formula to triangle \[\Delta ANB\] we get
\[\Rightarrow {{A}_{4}}=\dfrac{1}{2}\left( AN \right)\left( BN \right)\]
By substituting the required values we get
\[\begin{align}
  & \Rightarrow {{A}_{4}}=\dfrac{1}{2}\left( 8cm \right)\left( 5cm \right) \\
 & \Rightarrow {{A}_{4}}=20c{{m}^{2}} \\
\end{align}\]
Now let us consider the trapezium\[FMPE\].
Let us assume that the area of \[FMPE\] as \[{{A}_{5}}\].
We know that the area formula for a trapezium is
\[\text{Area of trapezium}=\dfrac{1}{2}\left( \text{distance between parallel sides} \right)\left( \text{sum of parallel sides} \right)\]
By using the above formula to trapezium \[FMPE\] we get
\[\Rightarrow {{A}_{5}}=\dfrac{1}{2}\left( MP \right)\left( MF+PE \right)\]
Here we have
\[\begin{align}
  & \Rightarrow MP=AP-AM \\
 & \Rightarrow MP=12cm-4cm \\
 & \Rightarrow MP=8cm \\
\end{align}\]
Now by substituting the required values in the area above we get
\[\begin{align}
  & \Rightarrow {{A}_{5}}=\dfrac{1}{2}\left( 8cm \right)\left( 5cm+6cm \right) \\
 & \Rightarrow {{A}_{5}}=\left( 4cm \right)\left( 11cm \right) \\
 & \Rightarrow {{A}_{5}}=44c{{m}^{2}} \\
\end{align}\]
Now let us consider the trapezium \[NQCB\]
Let us assume that the area of \[NQCB\] as \[{{A}_{6}}\]
By using the area formula of trapezium to trapezium \[NQBC\] we get
\[\Rightarrow {{A}_{6}}=\dfrac{1}{2}\left( NQ \right)\left( QC+NC \right)\]
Here we have
\[\begin{align}
  & \Rightarrow NQ=AQ-AN \\
 & \Rightarrow NQ=14cm-8cm \\
 & \Rightarrow NQ=6cm \\
\end{align}\]
Now by substituting the required values in the area above we get
\[\begin{align}
  & \Rightarrow {{A}_{6}}=\dfrac{1}{2}\left( 6cm \right)\left( 5cm+4cm \right) \\
 & \Rightarrow {{A}_{6}}=\left( 3cm \right)\left( 9cm \right) \\
 & \Rightarrow {{A}_{6}}=27c{{m}^{2}} \\
\end{align}\]
Now let us assume that the area of given figure as \[A\]
Here, we can see that the area of figure is divided into areas of triangles and trapeziums.
So, we can write the total area as
\[\Rightarrow A={{A}_{1}}+{{A}_{2}}+{{A}_{3}}+{{A}_{4}}+{{A}_{5}}+{{A}_{6}}\]
Now, by substituting the required areas in above equation we get
\[\begin{align}
  & \Rightarrow A=\left( 10+18+12+20+44+27 \right)c{{m}^{2}} \\
 & \Rightarrow A=131c{{m}^{2}} \\
\end{align}\]

Therefore, the total area of polygon ABCDEF is \[131c{{m}^{2}}\].

Note: The main mistake the students may do is calculation mistakes. Here, as there are many parts and calculating the area of each part may get wrong due to confusion. Calculating each part without confusion is the main part of solving this problem. Also in the formula of area of trapezium we have
\[\text{Area of trapezium}=\dfrac{1}{2}\left( \text{distance between parallel sides} \right)\left( \text{sum of parallel sides} \right)\]
Here, the distance between parallel sides is the perpendicular distance between the lines. But, students take the distance between the parallel sides as the length of the other side rather than the height. This part needs to be taken care of.