Question

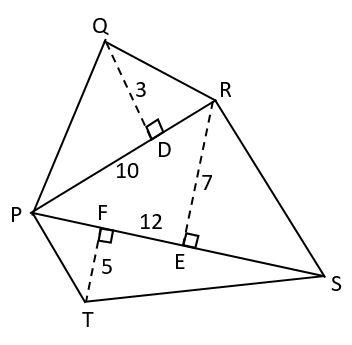
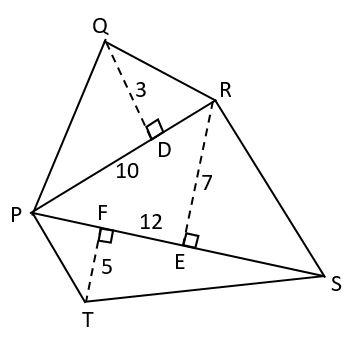
Find the area of pentagon$PQRST$in which $QD \bot PR,RE \bot PS$and $TF \bot PS$such that $PR = 10$cm, $PS = 12cm,$$QD = 3cm,$$RE = 7cm$and $TF = 5cm.$

Answer 1

Hint: It is better to understand a pentagon is a five-sided polygon in geometry. In the given question, the sides of the pentagon are different so do not use the properties of a regular pentagon.

Complete step by step Solution:
From the given figure,

We can observe that the pentagon can be separated into three triangles namely, $\Delta PQR,$ $\Delta PRS$and $\Delta PTS$
If we find the areas of these three triangles, then the sum of areas of all three angles will give us the area of the given pentagon i.e.
$ar(\Delta PQR) + ar(\Delta PRS) + ar(\Delta PTS) = ar(PQRST)$ . . . (1)
We know that, for a triangle with base b and perpendicular h, the area of a triangle is
$ = \dfrac{1}{2} \times b \times h$
In $\Delta PQR$
It is given that $QD \bot PR$
Thus we can write
\[ar(\Delta PQR) = \dfrac{1}{2} \times PR \times QD\]
Substituting the given values of PR and QD, we get
$ar(\Delta PQR) = \dfrac{1}{2} \times 10 \times 3$
$ \Rightarrow ar(\Delta PQR) = 15c{m^2}$ . . . (2)
In $\Delta PRS$
It is given that $RE \bot PS$
Thus we can write
\[ar(\Delta PRS) = \dfrac{1}{2} \times RE \times PS\]
Substituting the given values of RE and PS, we get
$ar(\Delta PRS) = \dfrac{1}{2} \times 7 \times 12$
$ \Rightarrow ar(\Delta PRS) = 42c{m^2}$ . . . (3)
In$\Delta PTS$
It is given that $TF \bot PS$
Thus we can write
$ar(\Delta PTS) = \dfrac{1}{2} \times PS \times TF$
Substituting the given values of PS and TF, we get

\[ar(\Delta PTS) = \dfrac{1}{2} \times 12 \times 5\]
$ \Rightarrow ar(\Delta PTS) = 30c{m^2}$ . . . (4)
From equation (1)
$ar(\Delta PQR) + ar(\Delta PRS) + ar(\Delta PTS) = ar(PQRST)$
Substituting the values of areas of respective triangles from equation (2), (3) and (4), we get
$ar(PQRST) = 15 + 42 + 30$
$ \Rightarrow ar(PQRST) = 87c{m^2}$
Hence, Area of pentagon$PQRST$is $87c{m^2}$
Note: This question was made easy by giving all the required values. But it is not always necessary that you will be given all this information. In such cases, to solve the problems on any polygon, you need to know their properties. Like, sum of angles and properties of regular polygons.