Question

How do you find the area of parallelogram with 2 sides and angle?

Answer 1

Hint: The formula for the area of a parallelogram is $ ab\sin \theta $ where a and b are length of 2 consecutive sides of the parallelogram. We can find the area of the parallelogram using this formula.

Complete step by step answer:
Let’s draw the figure of a parallelogram

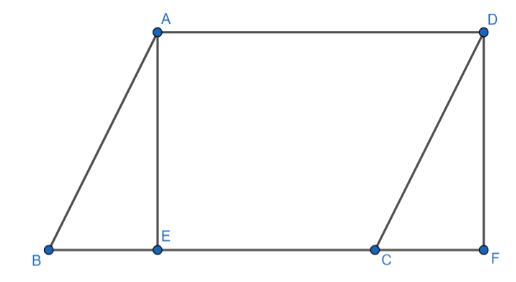
In the above figure, ABCD is a parallelogram and AE is the height of the parallelogram. DF is the height drawn from D.
Length of AE = length DF
And angle ABE = angle DCF
So triangle ABE and triangle DCF are congruent
So the area of ABE= area of DCF
Area of parallelogram ABCD = area of triangle ABE + area of trapezium AECD
We can replace ABE with the area of DCF in the above equation.
Area of parallelogram ABCD= area of triangle DCF + area of trapezium AECD

We can see in the figure area of triangle DCF + area of trapezium AECD is equal to the area of rectangle AEFD
We can write
Area of parallelogram ABCD = area of rectangle AEFD
We know that area of rectangle = length $ \times $ breath
So area of rectangle AEFD= $ EF\times AE $
 $ \Rightarrow EF=EC+CF $
CF is equal to BE from congruence of ABE and ACF
 $ \Rightarrow EF=EC+BE $
 $ \Rightarrow EF=BC $
Area of AEFD= $ BC\times AE $
Area of parallelogram ABCD= $ BC\times AE $
In triangle ABE, $ AE=AB\times \sin B $
Area of parallelogram ABCD= $ AB\times BC\times \sin B $
 $ \sin B=\sin A $ in ABCD as $ A+B={{180}^{\circ }} $
AB and BC are consecutive side of ABCD
So if 2 sides and one angle is given parallelogram the area will be product of 2 sides and sin of given angle.

Note:
If the vector form of 2 consecutive sides are given in a parallelogram then the area of parallelogram is $ \left| \overrightarrow{a}\times \overrightarrow{b} \right| $ where $ \overrightarrow{a} $ and $ \overrightarrow{b} $ are given vectors of sides. If all sides are same in a parallelogram it will became a rhombus area of rhombus is $ \dfrac{1}{2}\times $ product of diagonals.