Question

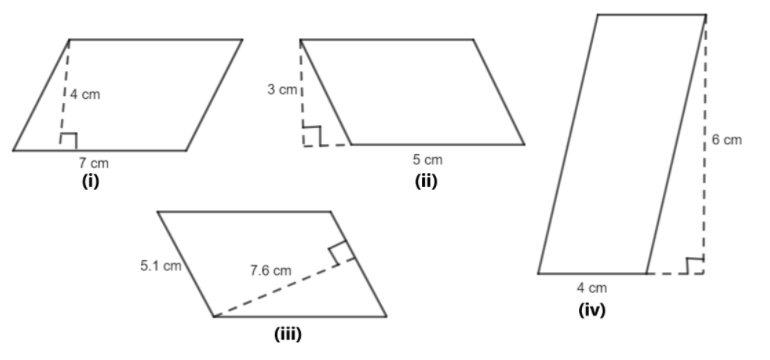
Find the area of each of the following parallelograms.

A.\[\left( i \right)\,28\,c{m^2}\,\,\left( {ii} \right)\,15\,c{m^2}\,\,\left( {iii} \right)\,38.76\,c{m^2}\,\,\left( {iv} \right)\,24\,c{m^2}\]
B.\[\left( i \right)\,2\,c{m^2}\,\,\left( {ii} \right)\,15\,c{m^2}\,\,\left( {iii} \right)\,38.76\,c{m^2}\,\,\left( {iv} \right)\,24\,c{m^2}\]
C.\[\left( i \right)\,28\,c{m^2}\,\,\left( {ii} \right)\,1\,c{m^2}\,\,\left( {iii} \right)\,38.76\,c{m^2}\,\,\left( {iv} \right)\,24\,c{m^2}\]
D.None of these

Answer 1

Hint: Here in this question, we have to find the area of the given parallelograms. To solve this by using a formula of area of parallelogram i.e., \[Area = base \times height\]. On substituting the given value of height and base in figures and by further simplification, we get the required value of area.

Complete step by step solution:
A parallelogram is a quadrilateral with two pairs of parallel sides. The opposite sides of a parallelogram are equal in length, and the opposite angles are equal in measure.
Let a parallelogram \[ABCD\], sides \[AB\parallel CD\] and \[AD\parallel BC\]. Draw a line AE perpendicular to the line DC i.e., \[AE \bot DC\] where \[AE\] be height if the parallelogram and \[AC\] or \[AB\] be the base of the parallelogram \[ABCD\].

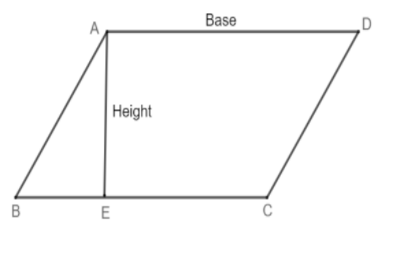
Area of a parallelogram is a region covered by a parallelogram in a two-dimensional plane. To find the area of the parallelogram, multiply the base of the perpendicular by its height.
\[\therefore \] The formula of area of a parallelogram:
\[ \Rightarrow \,\,Area = base \times height\]-----(1)
Now consider, the given parallelograms
In parallelogram (i), given \[base = 7cm\] and \[height = 4\,cm\].
By the formula of area
\[ \Rightarrow A = 7 \times 4\]
\[\therefore \,\]Area of parallelogram \[ = 28\,c{m^2}\].
In parallelogram (ii), given \[base = 5cm\] and \[height = 3\,cm\].
By the formula of area
\[ \Rightarrow A = 5 \times 3\]
\[\therefore \,\]Area of parallelogram \[ = 15\,c{m^2}\].
In parallelogram (iii), given \[base = 5.1cm\] and \[height = 7.6\,cm\].
By the formula of area
\[ \Rightarrow A = 5.1 \times 7.6\]
\[\therefore \,\]Area of parallelogram \[ = 38.76\,c{m^2}\].
In parallelogram (iv), given \[base = 4cm\] and \[height = 6\,cm\].
By the formula of area
\[ \Rightarrow A = 4 \times 6\]
\[\therefore \,\]Area of parallelogram \[ = 24\,c{m^2}\].
Hence, the area of parallelograms are \[\left( i \right)\,28\,c{m^2}\,\,\left( {ii} \right)\,15\,c{m^2}\,\,\left( {iii} \right)\,38.76\,c{m^2}\,\,\left( {iv} \right)\,24\,c{m^2}\]
Therefore, option (A) is correct
So, the correct answer is “Option A”.

Note: We can also determine the height and base of the parallelogram by using the formula of area. The formula is \[Area = base \times height\] we can alter the formula depending upon which one we want and remember the unit for the area will be the square of the unit of the length of the side of a parallelogram. We should not forget to write the unit.