Question

Find the area of an equilateral triangle inscribed in a circle of radius $ 10 $ cm?

Answer 1

Hint: In the given question, we need to find out the area of the triangle that is inscribed in a circle given the radius of the circle. We are also given that the triangle is equilateral in the question itself. So, we first need to find the side of the equilateral triangle and then find the area of the equilateral triangle by using the special formula $ \dfrac{{\sqrt 3 }}{4}{\left( a \right)^2} $ where a is the side of the equilateral triangle.

Complete step by step solution:

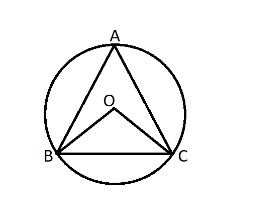
Let us consider the equilateral triangle ABC. Let O be the centre of the circle of radius \[10cm\] in which the t=equilateral triangle ABC is inscribed.
This means that the radii of the circumcircle of triangle ABC are \[10cm\] in length.
So, $ BO = CO = 10cm $
Now, we know that all the angles of an equilateral triangle ABC are equal and $ {60^ \circ } $ each.
So, $ \angle BAC = {60^ \circ } $
Now, using the property of the circle, we know that the angle made by a chord at the centre of the circle is double the angle made by the same chord in the segment corresponding to the side of the circle that contains the centre.
So, $ \angle BOC = {120^\circ } $
Also, $ \angle CBO = \angle OCB = {30^\circ } $ as the radius of the circle bisects the angles of the equilateral triangle ABC given to us.
Using sine rule in $ \Delta OBC $
 $ \dfrac{{\sin {{30}^\circ }}}{{10cm}} = \dfrac{{\sin {{120}^\circ }}}{{BC}} $
Putting the values of $ \sin {30^ \circ } $ and $ \sin {120^ \circ } $ ,
\[ \Rightarrow BC = \dfrac{{10 \times \dfrac{{\sqrt 3 }}{2}}}{{\dfrac{1}{2}}}\]
Simplifying the calculations, we get,
 $ \Rightarrow BC = 10\sqrt 3 $
Now, area of equilateral $ \Delta ABC $ $ = \dfrac{{\sqrt 3 }}{4}{\left( {10\sqrt 3 } \right)^2} $
 $ \Rightarrow \dfrac{{\sqrt 3 }}{4}\left( {300} \right)\,c{m^2} $
 $ \Rightarrow 75\sqrt 3 \,c{m^2} $
So, the area of an equilateral triangle inscribed in a circle of radius $ 10\,cm $ is $ 75\sqrt 3 \,c{m^2} $ .
So, the correct answer is “ $ 75\sqrt 3 \,c{m^2} $ ”.

Note: In the above problem, the side of the equilateral triangle can be found in various ways. The knowledge of trigonometric ratios and their applications can also be employed for finding the side of triangle ABC. Then, the area may also be calculated by using Heron’s formula or any other method.