Question

Find the area of a trapezium ABCD whose parallel sides are $AB = 19cm$, $DC = 9cm$ and non parallel sides are $BC = 8cm$ and $DA = 6cm$.

Answer 1

Hint: First we shall talk about the trapezoid. A trapezoid, also known as trapezium, is a quadrilateral consisting of one pair of parallel sides and one pair of non-parallel sides. It is a two-dimensional figure and it is also flat. Here, we call the parallel sides as the bases and non-parallel sides as legs.
Formula used:
The formula to calculate the area of the trapezoid is as follows.
Area of the trapezoid, $A = \dfrac{1}{2} \times \text{sum of parallel sides} \times h$
Where $h$ is the height which is the perpendicular distance between the parallel sides.

Complete step-by-step solution:

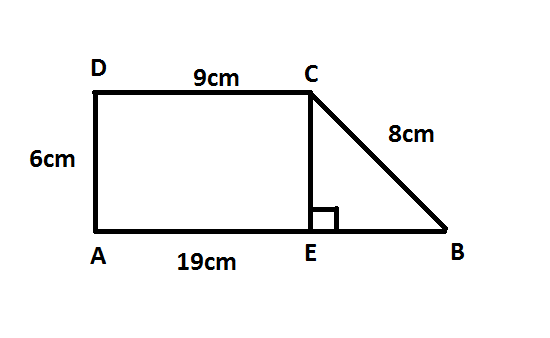
Let us construct a line $CE$ such that it is perpendicular to$AB$.
Therefore, $DC = AE$ .
Now we need to find the length of$EB$.
\[EB = AB - AE\]
Since, $AB = 19cm$ and $DC = 9cm$, $DC = AE$, we have
\[EB = 19 - 9\]
\[EB = 10\;cm\]
Now we need to find the length of $CE$ which is the height of the trapezium.
Here, we found that \[\Delta CEB\] is a right angled triangle.
Now, using Pythagoras theorem which is the square of the hypotenuse side is equal to the sum of the squares of the other two sides in a right angled triangle.
So, \[{(BC)^2} = {(CE)^2} + {(EB)^2}\]
Using the known values, we have,
\[{(8)^2} = {(CE)^2} + {(10)^2}\]
\[\Rightarrow 64 = {(CE)^2} + 100\]
\[\Rightarrow 100 - 64 = {(CE)^2}\]
$\Rightarrow CE = \sqrt {36} $
Therefore, \[CE = 6\;cm\]
It is given that parallel sides are $AB = 19cm$, $DC = 9cm$ and we found the perpendicular distance between the parallel sides, \[CE = 6\;cm\].
Now, using the formula, we have
Area of the trapezoid, $A = \dfrac{1}{2} \times \text{sum of parallel sides} \times h$
 \[ = \dfrac{1}{2}\times (9 + 19) \times 6\]
 \[ = \dfrac{1}{2} \times 28 \times 6\]
\[ = 14 \times 6\]
\[ = 84\;c{m^2}\]
Hence, the area of the trapezoid is \[84\;c{m^2}\].

Note: A trapezoid, also known as trapezium, is a quadrilateral consisting of one pair of parallel sides and one pair of non-parallel sides. The trapezoid height is the perpendicular distance between the parallel sides of a trapezoid. And the parallel sides and height are always perpendicular to each other.