Question

Find the area of a square whose perimeter is 24 cm.

Answer 1

Hint: First determine the side of the square with the help of the given perimeter. Since all the sides in a square are the same, the formula for its perimeter is $P = 4s$, where $s$ is the side of the square. Then apply the formula for the area of the square i.e. $A = {s^2}$ to get the answer.

Complete step-by-step answer:
According to the question, the perimeter of the given square is 24 cm.
We know that in square, all four sides are of equal length. Hence the formula for the perimeter of the square is:
$ \Rightarrow P = 4s$, where $s$ is the side of the square.
Applying this formula for the given perimeter, we’ll get:
$
   \Rightarrow 4s = 24{\text{ cm}} \\
   \Rightarrow s = \dfrac{{24}}{4}{\text{ cm}} = 6{\text{ cm }}.....{\text{(1)}}
 $
Thus the side of the square is of 6 cm length.

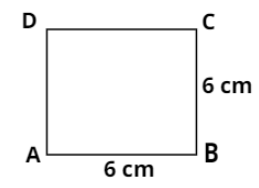
Now, we have to calculate the area of the square. We also know that the formula to determine the area of the square is $A = {s^2}$.
$ \Rightarrow A = {s^2}$
Applying this formula and putting the value of $s$ i.e. side length of the square from equation (1), we’ll get:
$
   \Rightarrow A = {\left( {6{\text{ cm}}} \right)^2} \\
   \Rightarrow A = 36{\text{ c}}{{\text{m}}^2}
 $

Therefore the area of the given square is $36{\text{ c}}{{\text{m}}^2}$.

Note: All the angles in a square are of ${90^ \circ }$. If all the sides of a quadrilateral are not equal but opposite sides are parallel and equal instead, along with all the angles ${90^ \circ }$ then the quadrilateral is called a rectangle. The perimeter of a rectangle is given by the formula $P = 2\left( {l + b} \right)$ whereas its area is calculated by the formula $A = l \times b$, where $l$ is the length and $b$ is the breadth of the rectangle.