Question

Find the area of a semicircle with the radius of 5 cm?

Answer 1

Hint: First we are going to use the formula of area of semicircle which is $\dfrac{\pi {{r}^{2}}}{2}$then we will substitute the value of r which is given in question in this area of semi circle expression and then simplify this area expression.

Complete step-by-step answer:
The below figure is of a circle with radius r.

Area of a circle$=\pi {{r}^{2}}$
And the semicircle is half of the circle.

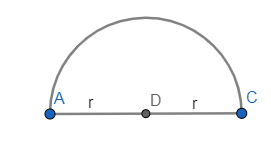
It’s like you cut the pizza in 2 equal halves so one of the half looks like a semicircle. In the below figure, the shaded region is the area of a semi circle.

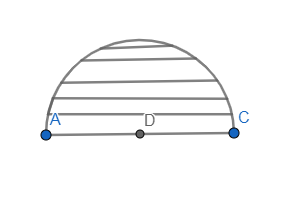
The formula for area of a semicircle is equal to:
$\text{Area of semicircle = }\dfrac{\pi {{r}^{2}}}{2}$
In the above expression r is the radius of the circle and it is given as 5 cm. So, substituting the value of radius in the above expression we get,
$\begin{align}
  & \text{Area = }\dfrac{3.14{{(5)}^{2}}}{2} \\
 & \text{ = }\dfrac{3.14(25)}{2} \\
 & \text{ = 39}\text{.25} \\
\end{align}$
Hence, the area of a semicircle is 39.25 ${cm}^{2}$.

Note: Given that the question is pretty basic but the possible mistakes that we encounter here are:
First, if the multiple choice question is given then the unit of area given in the options is not as same as the radius. So we have to convert the unit of radius into the unit of area as given in options like radius is given in metres and area is given in sq. cm so you have to convert the radius in metres to cm then put it in formula.
Another mistake that tends to happen is if diameter is given and we have to find the area so we tend to forget to convert the diameter into radius.
And always write the units of area like in ${cm}^{2}$ or whatever unit is asked.