Question

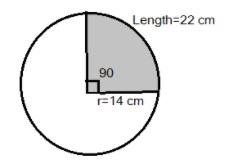
Find the area of a sector of a circle with a radius of 14 cm if the length of the corresponding arc is 22 cm.

Answer 1

Hint- Perimeter of a sector is the total length of the circumference of the circle subtended within the angle\[\theta \]. Perimeter is the sum of the total length of the arc and the two radii.
The length of the arc of a circle is a part of the total circumference of the circle given by$2\pi r$. In the given question, we have to find how much of the total circumference of the circle is subtended by the sector. The formula used for the length of the arc of a circle of radius $r$ and subtending $\theta $ degrees at the center of the circle is${P_{arc}} = 2\pi r \times \left( {\dfrac{\theta }{{360}}} \right)$ .
The area covered by the arc having radius r and subtending an angle of $\theta $ degrees at the center of the circle is calculated by using the formula${A_{arc}} = \pi {r^2}\left( {\dfrac{\theta }{{360}}} \right)$.

Substitute $r = 14$and ${P_{arc}} = 22$ in the formula ${P_{arc}} = 2\pi r \times \left( {\dfrac{\theta }{{360}}} \right)$ to determine the angle subtended by the arc at the center of the circle.

$
  {P_{arc}} = 2\pi r \times \left( {\dfrac{\theta }{{360}}} \right) \\
  22 = 2 \times \dfrac{{22}}{7} \times 14 \times \left( {\dfrac{\theta }{{360}}} \right) \\
  \left( {\dfrac{\theta }{{360}}} \right) = \dfrac{{22 \times 7}}{{2 \times 22 \times 14}} = \dfrac{1}{4} \\
  \theta = \dfrac{{360}}{4} = {90^0} \\
 $

Hence, the angle subtended by the arc having a radius of 14 cm and a length of 22 cm is${90^0}$.

Now, substitute $\theta = {90^0}$ and $r = 14$in the formula ${A_{arc}} = \pi {r^2}\left( {\dfrac{\theta }{{360}}} \right)$ to determine the area covered by the arc.
$
  {A_{arc}} = \pi {r^2}\left( {\dfrac{\theta }{{360}}} \right) \\
   = \dfrac{{22}}{7} \times {\left( {14} \right)^2} \times \left( {\dfrac{{90}}{{360}}} \right) \\
   = \dfrac{{22}}{7} \times 14 \times 14 \times \left( {\dfrac{1}{4}} \right) \\
   = 154{\text{ c}}{{\text{m}}^2} \\
 $

Hence, the area of the sector having a radius of 14 cm and an arc length of 22 cm is 154 square centimeters.

Note: Since the sector is just a part of the circle subtending an angle$\theta $ at the center, first find out by what factor of the full circle is covered by the sector using$\left( {\dfrac{\theta }{{360}}} \right)$. The Addition of the two radii arms with the length of the arc results in the total perimeter of the sector that is equivalent to${P_s} = 2\pi r \times \left( {\dfrac{\theta }{{360}}} \right) + 2r$. The formula can be used to determine the area of any part of the circle (for all the sectors of a circle) depending on the angle subtended in the center.