Answer
Verified449.4k+ views
Hint: A ring is the space between two concentric (same center) circles.
Area of the ring = Area of the outer circle - Area of the inner circle.
Area of a circle of radius r units is $\pi {{r}^{2}}\text{ sq. units}$ .
Complete step-by-step answer:
Let's say that the radius of the outer circle is ${{r}_{1}}=19\text{ cm}$ and the radius of the inner circle is ${{r}_{2}}=16\text{ cm}$ .
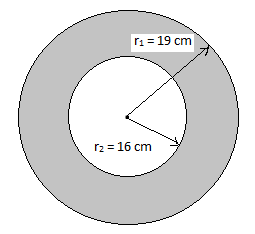
The area of the ring will be given by:
Area of the ring = Area of the outer circle - Area of the inner circle.
Using the formula for the area of a circle, we get:
= $\pi r_{1}^{2}-\pi r_{2}^{2}$
Taking out $\pi $ as the common factor:
= $\pi \left( r_{1}^{2}-r_{2}^{2} \right)$
= $\dfrac{22}{7}\left( {{19}^{2}}-{{16}^{2}} \right)$
Using the identity ${{a}^{2}}-{{b}^{2}}=(a+b)(a-b)$ , we get:
= $\dfrac{22}{7}\left( 19+16 \right)\left( 19-16 \right)$
= $\dfrac{22}{7}\times 35\times 3$
= $22\times 5\times 3$
= $330\text{ cm}^{2}$
Therefore, the correct answer option is A. $330\text{ cm}^{2}$ .
Note: The total circumference of the ring will be $2\pi ({{r}_{1}}+{{r}_{2}})$ .
Similar techniques can be used for finding the area of other shapes. e.g. Area of a pathway around a rectangular park.
A similar concept is used to calculate the volume of the material needed to construct a hollow solid.
Area of the ring = Area of the outer circle - Area of the inner circle.
Area of a circle of radius r units is $\pi {{r}^{2}}\text{ sq. units}$ .
Complete step-by-step answer:
Let's say that the radius of the outer circle is ${{r}_{1}}=19\text{ cm}$ and the radius of the inner circle is ${{r}_{2}}=16\text{ cm}$ .
The area of the ring will be given by:
Area of the ring = Area of the outer circle - Area of the inner circle.
Using the formula for the area of a circle, we get:
= $\pi r_{1}^{2}-\pi r_{2}^{2}$
Taking out $\pi $ as the common factor:
= $\pi \left( r_{1}^{2}-r_{2}^{2} \right)$
= $\dfrac{22}{7}\left( {{19}^{2}}-{{16}^{2}} \right)$
Using the identity ${{a}^{2}}-{{b}^{2}}=(a+b)(a-b)$ , we get:
= $\dfrac{22}{7}\left( 19+16 \right)\left( 19-16 \right)$
= $\dfrac{22}{7}\times 35\times 3$
= $22\times 5\times 3$
= $330\text{ cm}^{2}$
Therefore, the correct answer option is A. $330\text{ cm}^{2}$ .
Note: The total circumference of the ring will be $2\pi ({{r}_{1}}+{{r}_{2}})$ .
Similar techniques can be used for finding the area of other shapes. e.g. Area of a pathway around a rectangular park.
A similar concept is used to calculate the volume of the material needed to construct a hollow solid.