Question

Find the area of a regular polygon of 7 sides whose each side measures \[4\,\text{cm}\] and the circumradius is \[3\,\text{cm}\]. \[(\sqrt{5} = 2.236\].
A) \[31.304\,\text{cm}^{2}\]
B) \[31.804\,\text{cm}^{2}\]
C) \[31.304\,\text{m}^{2}\]
D) None of these

Answer 1

Hint: A regular polygon has all its sides and angles equal.
If the base and the altitude of a triangle are given as \[b\] and \[h\] respectively, then the area of the triangle is,
\[A=\dfrac{1}{2}\times b\times h\]

Complete step-by-step answer:
Given a regular polygon of 7 sides whose each side measures \[4\,\text{cm}\] and the circumradius is \[3\,\text{cm}\].
Let \[O\] be the centre of the polygon and, \[A\] and \[B\] be the adjacent vertex of the polygon as shown in the figure below.

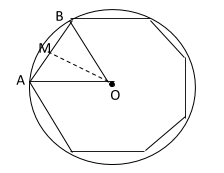
Now \[OA = 3\,\text{cm}\] and \[OB = 3\,\text{cm}\], as they are the circumradius. And \[AB = 4\,\text{cm}\].
As the angles are equal, so \[OM\] bisects the side \[AB\] into two equal parts. Therefore, \[AM = 2 = MB\].
Also, the triangle \[MOB\] is a right angled triangle. So, using the Pythagoras theorem, the length \[OM\] is calculated as,
\[OM^{2} = OB^{2} – MB^{2}\]
\[OM = \sqrt{(3)^{2}-(2)^{2}} = \sqrt{5}\]
Therefore, for the triangle \[AOB\], base is \[AB = 4\,\text{cm}\] and height is \[OM = \sqrt{5}\,\text{cm} = 2.236\,\text{cm}\].
So, the area of the triangle \[AOB\] is,
\[A=\dfrac{1}{2}\times 4\times 2.236=4.472\ \text{c}{{\text{m}}^{2}}\]
The area of the polygon is given by,
\[\text{Area}=7\times \text{Area}\ \text{of}\ \text{triangle}\ AOB\]
\[\text{Area}=7\times 4.472=31.304\ \text{c}{{\text{m}}^{2}}\]

Hence, the correct option is (A).

Note: When the polygon is a regular polygon of \[n\] sides, then the same method is applied to determine its area. Here the area of the triangle \[AOB\] would be multiplied by \[n\].