Question

Find the area of a regular pentagon whose each side is $8$ cm long and the radius of whose circumscribed circle is $7$ cm.

Answer 1

Hint: Use the formula of area of pentagon when circumscribed circle is given-
Area of pentagon= $\dfrac{{\text{n}}}{{\text{2}}} \times {{a \times }}\sqrt {{{\text{R}}^{\text{2}}}{\text{ - }}\dfrac{{{{\text{a}}^{\text{2}}}}}{{\text{4}}}} $ where n is the number of sides of the polygon, R is the radius of circumscribed triangle and ‘a’ is the length of the each side of polygon. Now we know that the Pentagon has five sides. A regular pentagon has equal five sides so put n=$5$ . Then by putting the given values in the formula and simplifying, get the area of the pentagon.

Complete step-by-step answer:
Given, the length of each side of regular pentagon=$8$ cm
The radius of the circumscribed circle =$7$ cm

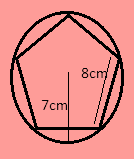
We know the formula of area of pentagon which circumscribed circle is given as-
Area of pentagon= $\dfrac{{\text{n}}}{{\text{2}}} \times {{a \times }}\sqrt {{{\text{R}}^{\text{2}}}{\text{ - }}\dfrac{{{{\text{a}}^{\text{2}}}}}{{\text{4}}}} $ where n is the number of sides of the polygon, R is the radius of circumscribed triangle and ‘a’ is the length of the each side of polygon.
Since the polygon is pentagon so n=$5$, a=$8$ cm and R=$7$ cm
On putting these values in the formula we get,
Area of pentagon=$\dfrac{5}{{\text{2}}} \times 8{{ \times }}\sqrt {{7^{\text{2}}}{\text{ - }}\dfrac{{{8^{\text{2}}}}}{{\text{4}}}} $
On solving we get,
Area of pentagon=$5 \times 4{{ \times }}\sqrt {{\text{49 - }}\dfrac{{64}}{{\text{4}}}} $
On simplifying we get,
Area of pentagon=$20{{ \times }}\sqrt {{\text{49 - }}16} $
On subtraction we get,
Area of pentagon=$20\sqrt {33} $
On further simplifying we get,
Then area of pentagon=$20 \times 5.74$
On multiplication we get,
Area of pentagon=$114.8$ ${\text{c}}{{\text{m}}^2}$.
Note: The properties of pentagon are as follows-
The sum of all interior angles in the pentagon is equal to ${540^\circ }$ .
If all sides and angles are equal to each other it is a regular polygon.
In a regular pentagon the interior angle is equal to ${108^\circ }$ and exterior angle is equal to ${72^\circ }$.