Question

Find the area of a quadrilateral whose sides are 12m, 5m, 6m, and 15m. The angle between the first two sides is 90. (use Heron’s Formula)
A.$20 + 2\sqrt {2805} $
B.$30 + 2\sqrt {805} $
C.$30 + 2\sqrt {374} $
D.$30 + 2\sqrt {1805} $

Answer 1

Hint: Quadrilateral: A quadrilateral can be defined as a closed, two-dimensional shape which has four straight sides. The polygon has four vertices or corners. Some examples of quadrilaterals are rectangle, square, rhombus, trapezium and kite.
As we know that the formula of Heron’s formula
$ \Rightarrow A = \sqrt {s(s - a)(s - b)(s - c)} $
Here,
s=semi perimeter
a=first side
b=second side
c=third side.

Complete step-by-step answer:
Given,
If ABCD is a quadrilateral
AB=12m
BC=5m
CD=6m
DA=15m
$\angle ABC = {90^o}$

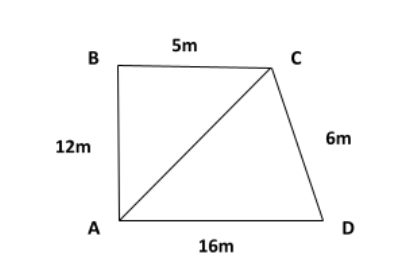
$ \Rightarrow Area\,of\,ABCD = Area\,of\,\vartriangle ABC + Area\,of\,\vartriangle ACD$
$In\,\vartriangle ABC,\angle B = {90^o}$
Therefore we use Pythagoras theorem to find the length of side AC.
As we know that Pythagoras theorem is given by
$ \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} $
Put the value in following equation
\[ \Rightarrow AC = \sqrt {{5^2} + {{12}^2}} \]
\[ \Rightarrow AC = \sqrt {25 + 144} \]
\[ \Rightarrow AC = \sqrt {169} \]
\[ \Rightarrow AC = \sqrt {13 \times 13} \]
Hence the length of side Ac is,
\[ \Rightarrow AC = 13m\]
So area of $\vartriangle ABC$ is,
$ \Rightarrow Area\,of\,\vartriangle ABC = \dfrac{1}{2} \times base \times height$
$ \Rightarrow Area\,of\,\vartriangle ABC = \dfrac{1}{2} \times AB \times BC$
Put the value in formula
$ \Rightarrow Area\,of\,\vartriangle ABC = \dfrac{1}{2} \times 12 \times 5$
$ \Rightarrow Area\,of\,\vartriangle ABC = 6 \times 5$
$ \Rightarrow Area\,of\,\vartriangle ABC = 30{m^2}$
So the area of $\vartriangle ABC$is $30{m^2}$
Now the area of $\vartriangle ACD$ is,
$ \Rightarrow s = \dfrac{{a + b + c}}{2}$
Here,
s=perimeter of triangle
Put the value
$ \Rightarrow s = \dfrac{{6 + 15 + 13}}{2}$
$ \Rightarrow s = 17m$
Apply Heron’s formula
$ \Rightarrow A = \sqrt {s(s - a)(s - b)(s - c)} $
Put the value in formula
$ \Rightarrow A = \sqrt {17(17 - 6)(17 - 13)(17 - 15)} $
$ \Rightarrow A = \sqrt {17 \times 11 \times 4 \times 2} $
$ \Rightarrow A = 2\sqrt {17 \times 11 \times 2} $
\[ \Rightarrow A = 2\sqrt {374} {m^2}\]
So the area of $\vartriangle ACD$ is\[2\sqrt {374} {m^2}\]
So the area of quadrilateral ABCD is
$ \Rightarrow Area\,of\,ABCD = Area\,of\,\vartriangle ABC + Area\,of\,\vartriangle ACD$
Put the value
$ \Rightarrow Area\,of\,ABCD = 30{m^2} + 2\sqrt {374} {m^2}$
$ \Rightarrow Area\,of\,ABCD = 30 + 2\sqrt {374} {m^2}$
So the answer is (C) $30 + 2\sqrt {374} $.
So, the correct answer is “Option C”.

Note: In quadrilateral the opposite sides are equal. All opposite sides are equal and parallel to each other. Diagonal bisect each other perpendicular. Sum of any two adjacent sides are${180^o}$. It has four right angles. The sum of all interior angles are${360^o}$. Quadrilaterals are coplanar.