
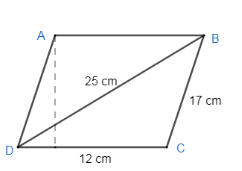
Find the area of a parallelogram given in Figure. Also find the length of the altitude from vertex A on the side DC. (in $c{{m}^{2}}$ )

Answer
603k+ views
Hint: To find the area of a parallelogram $ABCD=\text{Area of }\Delta \text{ABD+Area of }\Delta BCD$ . First determine the area of a triangle using Heron's formula $\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$ . Also determine the area of parallelogram by using the formula $Base\times Height$ to find the length of the altitude from vertex A on the side DC.
Complete step-by-step answer:
We know that the diagonal of a parallelogram divides it into two congruent triangles.
So, area of a parallelogram $ABCD=\text{Area of }\Delta \text{ABD+Area of }\Delta BCD$ .
Here, we will find the area of $\Delta BCD$
According to Heron’s formula the area of a triangle with sides a, b, & c is given as –
$\text{Area}=\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$ .
Where,
$s=\dfrac{\left( a+b+c \right)}{2}$ .
Here, we have from the figure –
$a=CD=12cm,\text{ }b=BC=17cm,\text{ c=BD=25cm}\text{.}$
So, we will get the value of s as –
$\begin{align}
& s=\dfrac{\left( 12+17+25 \right)}{2} \\
& =\dfrac{54}{2} \\
& =27 \\
\end{align}$
$\therefore s=27$
Now, we will put the value of a, b, c and s in the formula $\text{Area}=\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$ to find $\Delta BCD$.
$\text{Area}=\sqrt{27\times \left( 27-12 \right)\left( 27-17 \right)\left( 27-25 \right)}$
$\begin{align}
& =\sqrt{27\times 15\times 10\times 2} \\
& =\sqrt{8100} \\
& =90 \\
\end{align}$
$\therefore \text{Area of }\Delta BCD=90c{{m}^{2}}$
Since ABCD is a parallelogram,
$\text{Area of }\Delta BCD\text{=Area of }\Delta ABD$
Now, we will find the area of parallelogram.
Area of a parallelogram $ABCD=\text{Area of }\Delta \text{ABD+Area of }\Delta BCD$ .
$\begin{align}
& ABCD=90+90 \\
& =180c{{m}^{2}} \\
\end{align}$
$\therefore $ Area of a parallelogram $ABCD=180c{{m}^{2}}$
Next we will find the altitude of a parallelogram be h.
Let us consider the altitude of a parallelogram to be ‘h’.
Also, area of a parallelogram \[ABCD=\text{Base}\times \text{Height}\]
We know that the altitude of a parallelogram is also known as Height of a parallelogram.
Therefore,
Height of altitude from vertex A on side CD of the parallelogram $=\dfrac{\text{Area of parallelogram ABCD}}{Base}$ .
\[\begin{align}
& =\dfrac{180}{12} \\
& =15cm \\
\end{align}\]
Hence, the area of a parallelogram for the given figure is $180c{{m}^{2}}$ and the altitude from vertex A on side CD is 15 cm.
Note: We have taken the area of both triangles as the same here, but if a student doesn't know that, they can find it separately and then add them together. The mistake of finding an area of parallelogram as \[17\text{ }cm\text{ }\times \text{ }12\text{ }cm\] should be avoided, it is not correct at all. A parallelogram is a simple quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure. Opposite sides of a parallelogram are parallel and so will never intersect.
Complete step-by-step answer:
We know that the diagonal of a parallelogram divides it into two congruent triangles.
So, area of a parallelogram $ABCD=\text{Area of }\Delta \text{ABD+Area of }\Delta BCD$ .
Here, we will find the area of $\Delta BCD$
According to Heron’s formula the area of a triangle with sides a, b, & c is given as –
$\text{Area}=\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$ .
Where,
$s=\dfrac{\left( a+b+c \right)}{2}$ .
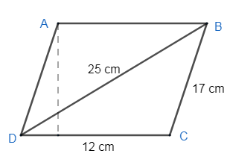
Here, we have from the figure –

$a=CD=12cm,\text{ }b=BC=17cm,\text{ c=BD=25cm}\text{.}$
So, we will get the value of s as –
$\begin{align}
& s=\dfrac{\left( 12+17+25 \right)}{2} \\
& =\dfrac{54}{2} \\
& =27 \\
\end{align}$
$\therefore s=27$
Now, we will put the value of a, b, c and s in the formula $\text{Area}=\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$ to find $\Delta BCD$.
$\text{Area}=\sqrt{27\times \left( 27-12 \right)\left( 27-17 \right)\left( 27-25 \right)}$
$\begin{align}
& =\sqrt{27\times 15\times 10\times 2} \\
& =\sqrt{8100} \\
& =90 \\
\end{align}$
$\therefore \text{Area of }\Delta BCD=90c{{m}^{2}}$
Since ABCD is a parallelogram,
$\text{Area of }\Delta BCD\text{=Area of }\Delta ABD$
Now, we will find the area of parallelogram.
Area of a parallelogram $ABCD=\text{Area of }\Delta \text{ABD+Area of }\Delta BCD$ .
$\begin{align}
& ABCD=90+90 \\
& =180c{{m}^{2}} \\
\end{align}$
$\therefore $ Area of a parallelogram $ABCD=180c{{m}^{2}}$
Next we will find the altitude of a parallelogram be h.
Let us consider the altitude of a parallelogram to be ‘h’.
Also, area of a parallelogram \[ABCD=\text{Base}\times \text{Height}\]
We know that the altitude of a parallelogram is also known as Height of a parallelogram.
Therefore,
Height of altitude from vertex A on side CD of the parallelogram $=\dfrac{\text{Area of parallelogram ABCD}}{Base}$ .
\[\begin{align}
& =\dfrac{180}{12} \\
& =15cm \\
\end{align}\]
Hence, the area of a parallelogram for the given figure is $180c{{m}^{2}}$ and the altitude from vertex A on side CD is 15 cm.
Note: We have taken the area of both triangles as the same here, but if a student doesn't know that, they can find it separately and then add them together. The mistake of finding an area of parallelogram as \[17\text{ }cm\text{ }\times \text{ }12\text{ }cm\] should be avoided, it is not correct at all. A parallelogram is a simple quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure. Opposite sides of a parallelogram are parallel and so will never intersect.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who is eligible for RTE class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE




