Question

How do you find the area of a ${{120}^{\circ }}$ sector of a circle whose radius is $6$ ?

Answer 1

Hint: In this question we have been asked to find the area of a ${{120}^{{}^\circ }}$ sector of a circle whose radius is $6$ . We know that the formula for finding the area of a $\theta $ sector of a circle whose radius is $r$ given as $\dfrac{\theta }{{{360}^{\circ }}}\times \pi {{r}^{2}}$ .

Complete step by step solution:
Now considering from the question we need to find the area of a ${{120}^{{}^\circ }}$ sector of a circle whose radius is $6$ .
Form the basics of circles concept, we know that the formula for finding the area of a $\theta $ sector of a circle whose radius is $r$ given as $\dfrac{\theta }{{{360}^{\circ }}}\times \pi {{r}^{2}}$ .
By applying this formula here we will have $Area=\dfrac{\theta }{{{360}^{\circ }}}\times \pi {{r}^{2}}\Rightarrow \dfrac{{{120}^{\circ }}}{{{360}^{\circ }}}\times \pi {{\left( 6 \right)}^{2}}$ .

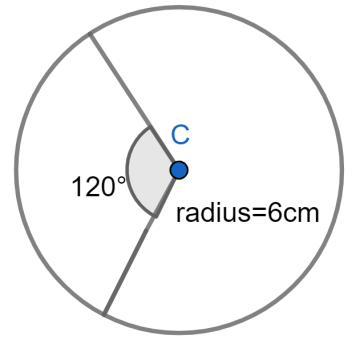
By further simplifying this expression we will have $\Rightarrow \dfrac{{{120}^{\circ }}}{{{360}^{\circ }}}\times \pi {{\left( 6 \right)}^{2}}=\pi \left( 12 \right)\Rightarrow 37.7c{{m}^{2}}$ .
Therefore we can conclude that the area of a ${{120}^{\circ }}$ sector of a circle whose radius is $6$ is given as $37.7$ .

Note: In this question solving process we should be sure with our calculations and concepts that we apply. This is a very simple question and can be solved in a short span of time and very few mistakes are possible during the process of finding the answer. Similarly we can find the area of full circle using the formula $\pi {{r}^{2}}$ semicircle $\dfrac{1}{2}\pi {{r}^{2}}$ and a quarter of a circle is $\dfrac{1}{4}\pi {{r}^{2}}$ where $r$ is the radius of the circle. For the given circle it is given that its radius is $6$ so its area of full circle will be $\pi {{\left( r \right)}^{2}}=\pi {{\left( 6 \right)}^{2}}\Rightarrow 36\pi =113.14$ .