
How do you find the area inside of the circle $r=3\sin \theta $ and outside the cardioid $r=1+\sin \theta $ ?
Answer
546.6k+ views
Hint: We are given to find the area due to the intersection of the circle and the cardioid and our required region is defined to be inside the circle but outside the cardioid. In such a situation, we must first find the points of intersection of the circle and the cardioid. Then we shall perform integration to find the area of the circle and the cardioid separately. Then we will subtract those two to obtain the final result.
Complete step by step solution:
Let us find the points of intersection by substituting $r=3\sin \theta $ in $r=1+\sin \theta $.
$\begin{align}
& \Rightarrow 3\sin \theta =1+\sin \theta \\
& \Rightarrow 2\sin \theta =1 \\
\end{align}$
Dividing both sides by 2, we get
$\begin{align}
& \Rightarrow \sin \theta =\dfrac{1}{2} \\
& \Rightarrow \theta ={{\sin }^{-1}}\dfrac{1}{2} \\
\end{align}$
If $\theta \in \left[ 0,2\pi \right]$ , we get $\theta =\dfrac{\pi }{6},\dfrac{5\pi }{6}$
Thus, we have to find the area of circle and cardioid one-by-one respectively for $\theta \in \left[ \dfrac{\pi }{6},\dfrac{5\pi }{6} \right]$.
We know that the area of a polar curve is given as $\dfrac{1}{2}\int{{{r}^{2}}}.d\theta $ when the polar equations of any curve are given.
First, we shall find the area $\left( {{A}_{1}} \right)$ of circle, $r=3\sin \theta $.
$\Rightarrow {{A}_{1}}=\dfrac{1}{2}\int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{{{\left( 3\sin \theta \right)}^{2}}}.d\theta $
$\begin{align}
& \Rightarrow {{A}_{1}}=\dfrac{1}{2}\int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{9{{\sin }^{2}}\theta }.d\theta \\
& \Rightarrow {{A}_{1}}=\dfrac{9}{2}\int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{{{\sin }^{2}}\theta }.d\theta \\
\end{align}$
Here, we shall use the trigonometric property, ${{\sin }^{2}}\theta =\dfrac{1-\cos 2\theta }{2}$ and get:
\[\begin{align}
& \Rightarrow {{A}_{1}}=\dfrac{9}{2}\int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{\left( \dfrac{1-\cos 2\theta }{2} \right)}.d\theta \\
& \Rightarrow {{A}_{1}}=\dfrac{9}{4}\int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{1-\cos 2\theta }.d\theta \\
& \Rightarrow {{A}_{1}}=\dfrac{9}{4}\left[ \int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{1.d\theta -\int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{\cos 2\theta .d\theta }} \right] \\
\end{align}\]
We know that $\int{1.dx=x+C}$ and $\int{\cos ax.dx=\dfrac{\sin ax}{a}+C}$, thus we shall use this further
$\begin{align}
& \Rightarrow {{A}_{1}}=\dfrac{9}{4}\left[ \left. \theta \right|_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}-\left. \dfrac{\sin 2\theta }{2} \right|_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}} \right] \\
& \Rightarrow {{A}_{1}}=\dfrac{9}{4}\left( \dfrac{5\pi }{6}-\dfrac{\pi }{6}-\dfrac{\sin 2\dfrac{5\pi }{6}}{2}+\dfrac{\sin 2\dfrac{\pi }{6}}{2} \right) \\
& \Rightarrow {{A}_{1}}=\dfrac{9}{4}\left( \dfrac{4\pi }{6}+\dfrac{\sin \dfrac{\pi }{3}-\sin \dfrac{5\pi }{3}}{2} \right) \\
\end{align}$
Substituting the value of $\sin \dfrac{\pi }{3}=\dfrac{\sqrt{3}}{2}$ and $\sin \dfrac{5\pi }{3}=-\dfrac{\sqrt{3}}{2}$, we get
$\begin{align}
& \Rightarrow {{A}_{1}}=\dfrac{9}{4}\left( \dfrac{4\pi }{6}+\dfrac{\dfrac{\sqrt{3}}{2}-\left( -\dfrac{\sqrt{3}}{2} \right)}{2} \right) \\
& \Rightarrow {{A}_{1}}=\dfrac{9}{4}\left( \dfrac{2\pi }{3}+\dfrac{\sqrt{3}}{2} \right) \\
\end{align}$
$\Rightarrow {{A}_{1}}=\dfrac{3\pi }{2}+\dfrac{9\sqrt{3}}{8}$ ……………………. (1)
Now, we shall find the area $\left( {{A}_{2}} \right)$ of circle, $r=1+\sin \theta $.
$\Rightarrow {{A}_{2}}=\dfrac{1}{2}\int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{{{\left( 1+\sin \theta \right)}^{2}}}.d\theta $
$\Rightarrow {{A}_{2}}=\dfrac{1}{2}\int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{1+{{\sin }^{2}}\theta }+2\sin \theta .d\theta $
Here, we shall use the trigonometric property, ${{\sin }^{2}}\theta =\dfrac{1-\cos 2\theta }{2}$ and get:
\[\begin{align}
& \Rightarrow {{A}_{2}}=\dfrac{1}{2}\int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{1+\left( \dfrac{1-\cos 2\theta }{2} \right)}+2\sin \theta .d\theta \\
& \Rightarrow {{A}_{2}}=\dfrac{1}{4}\int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{2+1-\cos 2\theta +4\sin \theta }.d\theta \\
& \Rightarrow {{A}_{2}}=\dfrac{1}{4}\left[ \int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{3.d\theta -\int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{\cos 2\theta .d\theta +4\int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{\sin \theta .d\theta }}} \right] \\
\end{align}\]
We know that $\int{1.dx=x+C}$, $\int{\sin x.dx=-\cos x+C}$ and $\int{\cos ax.dx=\dfrac{\sin ax}{a}+C}$, thus we shall use this further
$\begin{align}
& \Rightarrow {{A}_{2}}=\dfrac{1}{4}\left[ \left. 3\theta \right|_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}-\left. \dfrac{\sin 2\theta }{2} \right|_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}-\left. 4\cos \theta \right|_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}} \right] \\
& \Rightarrow {{A}_{2}}=\dfrac{1}{4}\left( \dfrac{15\pi }{6}-\dfrac{3\pi }{6}-\dfrac{\sin 2\dfrac{5\pi }{6}}{2}+\dfrac{\sin 2\dfrac{\pi }{6}}{2}-4\cos \dfrac{5\pi }{6}+4\cos \dfrac{\pi }{6} \right) \\
& \Rightarrow {{A}_{2}}=\dfrac{1}{4}\left( \dfrac{12\pi }{6}+\dfrac{\sin \dfrac{\pi }{3}-\sin \dfrac{5\pi }{3}}{2}+4\cos \dfrac{\pi }{6}-4\cos \dfrac{5\pi }{6} \right) \\
\end{align}$
Substituting the value of $\cos \dfrac{\pi }{6}=\dfrac{\sqrt{3}}{2}$, $\cos \dfrac{5\pi }{6}=-\dfrac{\sqrt{3}}{2}$ $\sin \dfrac{\pi }{3}=\dfrac{\sqrt{3}}{2}$ and $\sin \dfrac{5\pi }{3}=-\dfrac{\sqrt{3}}{2}$, we get
$\begin{align}
& \Rightarrow {{A}_{2}}=\dfrac{1}{4}\left( 2\pi +\dfrac{\dfrac{\sqrt{3}}{2}-\left( -\dfrac{\sqrt{3}}{2} \right)}{2}+4\dfrac{\sqrt{3}}{2}-\left( -4\dfrac{\sqrt{3}}{2} \right) \right) \\
& \Rightarrow {{A}_{2}}=\dfrac{1}{4}\left( 2\pi +\dfrac{\sqrt{3}}{2}+4\sqrt{3} \right) \\
& \Rightarrow {{A}_{2}}=\dfrac{1}{4}\left( 2\pi +\dfrac{\sqrt{3}+8\sqrt{3}}{2} \right) \\
\end{align}$
$\Rightarrow {{A}_{2}}=\dfrac{\pi }{2}+\dfrac{9\sqrt{3}}{8}$ ……………………. (2)
Therefore, the required area, $A={{A}_{1}}-{{A}_{2}}$
Substituting value of ${{A}_{1}}$ and ${{A}_{2}}$ from (1) and (2), we get
$\begin{align}
& \Rightarrow A=\dfrac{3\pi }{2}+\dfrac{9\sqrt{3}}{8}-\left( \dfrac{\pi }{2}+\dfrac{9\sqrt{3}}{8} \right) \\
& \Rightarrow A=\dfrac{3\pi }{2}-\dfrac{\pi }{2} \\
& \Rightarrow A=\pi \\
\end{align}$
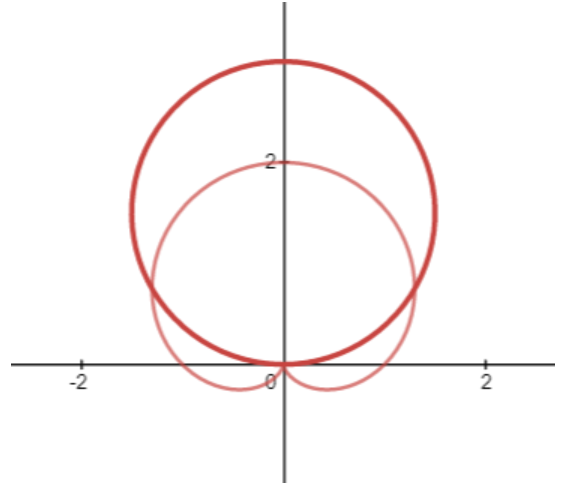
Hence, the area inside of the circle $r=3\sin \theta $ and outside the cardioid $r=1+\sin \theta $ is $\pi $ square units.
Note: Another method of solving this problem was by sketching the graph of the two curves and then marking the point of intersection from it. We could further simultaneously integrate to find the areas of each curve. However, the possible mistakes one could make is during the calculation part of the integrals as it consists of a lot of terms to be taken care of at the same time.
Complete step by step solution:
Let us find the points of intersection by substituting $r=3\sin \theta $ in $r=1+\sin \theta $.
$\begin{align}
& \Rightarrow 3\sin \theta =1+\sin \theta \\
& \Rightarrow 2\sin \theta =1 \\
\end{align}$
Dividing both sides by 2, we get
$\begin{align}
& \Rightarrow \sin \theta =\dfrac{1}{2} \\
& \Rightarrow \theta ={{\sin }^{-1}}\dfrac{1}{2} \\
\end{align}$
If $\theta \in \left[ 0,2\pi \right]$ , we get $\theta =\dfrac{\pi }{6},\dfrac{5\pi }{6}$
Thus, we have to find the area of circle and cardioid one-by-one respectively for $\theta \in \left[ \dfrac{\pi }{6},\dfrac{5\pi }{6} \right]$.
We know that the area of a polar curve is given as $\dfrac{1}{2}\int{{{r}^{2}}}.d\theta $ when the polar equations of any curve are given.
First, we shall find the area $\left( {{A}_{1}} \right)$ of circle, $r=3\sin \theta $.
$\Rightarrow {{A}_{1}}=\dfrac{1}{2}\int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{{{\left( 3\sin \theta \right)}^{2}}}.d\theta $
$\begin{align}
& \Rightarrow {{A}_{1}}=\dfrac{1}{2}\int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{9{{\sin }^{2}}\theta }.d\theta \\
& \Rightarrow {{A}_{1}}=\dfrac{9}{2}\int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{{{\sin }^{2}}\theta }.d\theta \\
\end{align}$
Here, we shall use the trigonometric property, ${{\sin }^{2}}\theta =\dfrac{1-\cos 2\theta }{2}$ and get:
\[\begin{align}
& \Rightarrow {{A}_{1}}=\dfrac{9}{2}\int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{\left( \dfrac{1-\cos 2\theta }{2} \right)}.d\theta \\
& \Rightarrow {{A}_{1}}=\dfrac{9}{4}\int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{1-\cos 2\theta }.d\theta \\
& \Rightarrow {{A}_{1}}=\dfrac{9}{4}\left[ \int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{1.d\theta -\int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{\cos 2\theta .d\theta }} \right] \\
\end{align}\]
We know that $\int{1.dx=x+C}$ and $\int{\cos ax.dx=\dfrac{\sin ax}{a}+C}$, thus we shall use this further
$\begin{align}
& \Rightarrow {{A}_{1}}=\dfrac{9}{4}\left[ \left. \theta \right|_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}-\left. \dfrac{\sin 2\theta }{2} \right|_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}} \right] \\
& \Rightarrow {{A}_{1}}=\dfrac{9}{4}\left( \dfrac{5\pi }{6}-\dfrac{\pi }{6}-\dfrac{\sin 2\dfrac{5\pi }{6}}{2}+\dfrac{\sin 2\dfrac{\pi }{6}}{2} \right) \\
& \Rightarrow {{A}_{1}}=\dfrac{9}{4}\left( \dfrac{4\pi }{6}+\dfrac{\sin \dfrac{\pi }{3}-\sin \dfrac{5\pi }{3}}{2} \right) \\
\end{align}$
Substituting the value of $\sin \dfrac{\pi }{3}=\dfrac{\sqrt{3}}{2}$ and $\sin \dfrac{5\pi }{3}=-\dfrac{\sqrt{3}}{2}$, we get
$\begin{align}
& \Rightarrow {{A}_{1}}=\dfrac{9}{4}\left( \dfrac{4\pi }{6}+\dfrac{\dfrac{\sqrt{3}}{2}-\left( -\dfrac{\sqrt{3}}{2} \right)}{2} \right) \\
& \Rightarrow {{A}_{1}}=\dfrac{9}{4}\left( \dfrac{2\pi }{3}+\dfrac{\sqrt{3}}{2} \right) \\
\end{align}$
$\Rightarrow {{A}_{1}}=\dfrac{3\pi }{2}+\dfrac{9\sqrt{3}}{8}$ ……………………. (1)
Now, we shall find the area $\left( {{A}_{2}} \right)$ of circle, $r=1+\sin \theta $.
$\Rightarrow {{A}_{2}}=\dfrac{1}{2}\int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{{{\left( 1+\sin \theta \right)}^{2}}}.d\theta $
$\Rightarrow {{A}_{2}}=\dfrac{1}{2}\int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{1+{{\sin }^{2}}\theta }+2\sin \theta .d\theta $
Here, we shall use the trigonometric property, ${{\sin }^{2}}\theta =\dfrac{1-\cos 2\theta }{2}$ and get:
\[\begin{align}
& \Rightarrow {{A}_{2}}=\dfrac{1}{2}\int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{1+\left( \dfrac{1-\cos 2\theta }{2} \right)}+2\sin \theta .d\theta \\
& \Rightarrow {{A}_{2}}=\dfrac{1}{4}\int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{2+1-\cos 2\theta +4\sin \theta }.d\theta \\
& \Rightarrow {{A}_{2}}=\dfrac{1}{4}\left[ \int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{3.d\theta -\int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{\cos 2\theta .d\theta +4\int\limits_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}{\sin \theta .d\theta }}} \right] \\
\end{align}\]
We know that $\int{1.dx=x+C}$, $\int{\sin x.dx=-\cos x+C}$ and $\int{\cos ax.dx=\dfrac{\sin ax}{a}+C}$, thus we shall use this further
$\begin{align}
& \Rightarrow {{A}_{2}}=\dfrac{1}{4}\left[ \left. 3\theta \right|_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}-\left. \dfrac{\sin 2\theta }{2} \right|_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}}-\left. 4\cos \theta \right|_{\dfrac{\pi }{6}}^{\dfrac{5\pi }{6}} \right] \\
& \Rightarrow {{A}_{2}}=\dfrac{1}{4}\left( \dfrac{15\pi }{6}-\dfrac{3\pi }{6}-\dfrac{\sin 2\dfrac{5\pi }{6}}{2}+\dfrac{\sin 2\dfrac{\pi }{6}}{2}-4\cos \dfrac{5\pi }{6}+4\cos \dfrac{\pi }{6} \right) \\
& \Rightarrow {{A}_{2}}=\dfrac{1}{4}\left( \dfrac{12\pi }{6}+\dfrac{\sin \dfrac{\pi }{3}-\sin \dfrac{5\pi }{3}}{2}+4\cos \dfrac{\pi }{6}-4\cos \dfrac{5\pi }{6} \right) \\
\end{align}$
Substituting the value of $\cos \dfrac{\pi }{6}=\dfrac{\sqrt{3}}{2}$, $\cos \dfrac{5\pi }{6}=-\dfrac{\sqrt{3}}{2}$ $\sin \dfrac{\pi }{3}=\dfrac{\sqrt{3}}{2}$ and $\sin \dfrac{5\pi }{3}=-\dfrac{\sqrt{3}}{2}$, we get
$\begin{align}
& \Rightarrow {{A}_{2}}=\dfrac{1}{4}\left( 2\pi +\dfrac{\dfrac{\sqrt{3}}{2}-\left( -\dfrac{\sqrt{3}}{2} \right)}{2}+4\dfrac{\sqrt{3}}{2}-\left( -4\dfrac{\sqrt{3}}{2} \right) \right) \\
& \Rightarrow {{A}_{2}}=\dfrac{1}{4}\left( 2\pi +\dfrac{\sqrt{3}}{2}+4\sqrt{3} \right) \\
& \Rightarrow {{A}_{2}}=\dfrac{1}{4}\left( 2\pi +\dfrac{\sqrt{3}+8\sqrt{3}}{2} \right) \\
\end{align}$
$\Rightarrow {{A}_{2}}=\dfrac{\pi }{2}+\dfrac{9\sqrt{3}}{8}$ ……………………. (2)
Therefore, the required area, $A={{A}_{1}}-{{A}_{2}}$
Substituting value of ${{A}_{1}}$ and ${{A}_{2}}$ from (1) and (2), we get
$\begin{align}
& \Rightarrow A=\dfrac{3\pi }{2}+\dfrac{9\sqrt{3}}{8}-\left( \dfrac{\pi }{2}+\dfrac{9\sqrt{3}}{8} \right) \\
& \Rightarrow A=\dfrac{3\pi }{2}-\dfrac{\pi }{2} \\
& \Rightarrow A=\pi \\
\end{align}$

Hence, the area inside of the circle $r=3\sin \theta $ and outside the cardioid $r=1+\sin \theta $ is $\pi $ square units.
Note: Another method of solving this problem was by sketching the graph of the two curves and then marking the point of intersection from it. We could further simultaneously integrate to find the areas of each curve. However, the possible mistakes one could make is during the calculation part of the integrals as it consists of a lot of terms to be taken care of at the same time.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




