Question

How do you find the area in the first quadrant bounded by $ y = {x^{ - 2}} $ and $ y = \dfrac{{17}}{4} - {x^2} $ ?

Answer 1

Hint: The following type of question is solved first by plotting out the relevant curves on the graph in the coordinate plane. Then we find their intersection points of the two curves with each other by substituting the value of one function into the other function and then the definite integrating in the intervals in which the curve is the same to find the area of the curves. The area obtained will be in square units of the graph but we will generically write square units.

Complete step by step solution:
The following curves are first plotted on the graph,

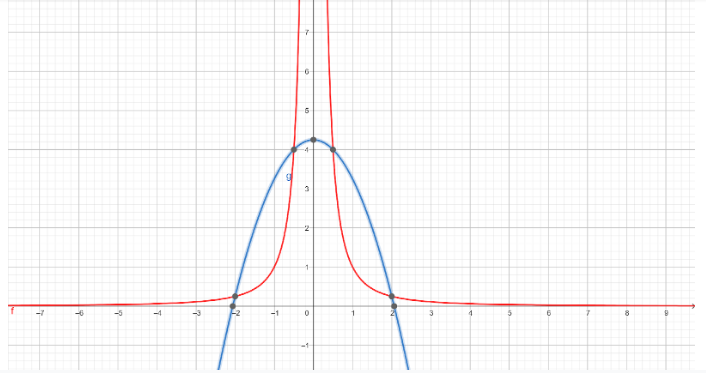
The graph in red is for $ y = {x^{ - 2}} $ while the graph in blue is of parabola $ y = \dfrac{{17}}{4} - {x^2} $
Then we will find the points of intersection of the parabola and the hyperbola:
We start by putting both the values of $ y $ equal we get:
 $ {x^{ - 2}} = \dfrac{{17}}{4} - {x^2} $
Upon solving the above equation we reach,
 $ 4{x^4} - 17{x^2} + 4 = 0 $
Since it has become a biquadratic equation we will put $ u = {x^2} $
Then we will get,
 $ 4{u^2} - 17u + 4 = 0 $
 $ \left( {4u - 1} \right)\left( {u - 4} \right) = 0 $
Upon solving for $ u $ we will get
 $ u = \dfrac{1}{4}\;\:{\text{or}}\;\:4 $ and then we get value of $ x $ as
 $ x = \pm \dfrac{1}{2}\;\:{\text{or}}\;\:x = \pm 2 $
Thus we see both from the graph and above solution that the curves cut each other 4 times.
Now to find the area in the first quadrant our two points of interest become $ 2 $ and $ \dfrac{1}{2} $ so upon integration we use these boundary conditions. The area will now be given by blue expression in the graph minus the the graph in red so we write our expression as:
 $ A = \mathop \int \nolimits_{\dfrac{1}{2}}^2 \dfrac{{17}}{4} - {x^2} - \left( {{x^{ - 2}}} \right)dx $
Which upon solving becomes,
 $ A = \left[ {\dfrac{{17}}{4}\left( x \right) - \dfrac{1}{3}{x^3} + {x^{ - 1}}} \right]_{\dfrac{1}{2}}^2 $
This will then be evaluated by putting the boundary conditions,
 $ A = \dfrac{{17}}{4}\left( 2 \right) - \dfrac{1}{3}{\left( 2 \right)^3} + {2^{ - 1}} - \left( {\dfrac{{17}}{4}\left( {\dfrac{1}{2}} \right) - \dfrac{1}{3}{{\left( {\dfrac{1}{2}} \right)}^3} + {{\left( {\dfrac{1}{2}} \right)}^{ - 1}}} \right) $
 $ A = 7 - \dfrac{8}{3} - \dfrac{{50}}{{24}} $
Thus after solving above expression we get our area as,
 $ A = \dfrac{{54}}{{24}} = \dfrac{9}{4}{\text{square units}} $
So, the correct answer is “ $ A = \dfrac{{54}}{{24}} = \dfrac{9}{4}{\text{square units}} $ ”.

Note: It is very important to find the point of intersection in the given types of questions otherwise we will not get the boundary conditions that will tell upto which limits we have to integrate. Also note here we have neglected negative values of $ x $ since we had to find the area in the first quadrant.