Question

Find the area enclosed between \[{{y}^{2}}=x\]and \[y=x\]. Choose the correct option.
A. \[\dfrac{2}{3}\]sq unit
B. \[\dfrac{1}{2}\]sq unit
C. \[\dfrac{1}{3}\]sq unit
D. \[\dfrac{1}{6}\]sq unit

Answer 1

Hint: Use the concept that the area between curves is the area between a curve \[f\left( x \right)\]and a curve \[g\left( x \right)\]on an interval \[\left[ a,\;b \right]\]given by \[A=\int_{a}^{b}{|}f\left( x \right)-g\left( x \right)|dx\]. So, here \[f\left( x \right)\]is found from\[{{y}^{2}}=x\]and \[g\left( x \right)\]is found from \[y=x\]. Next, we will have to find the intersection points of the functions\[{{y}^{2}}=x\]and \[y=x\], so as to get a and b. The X-coordinate of the first intersection point is a and the X-coordinate of the second intersection point is b.

Complete step-by-step answer:
In the question, we have to find the area enclosed between \[{{y}^{2}}=x\]and \[y=x\]. Now, it is already known that the area between curves \[f\left( x \right)\]and a curve \[g\left( x \right)\]on an interval \[\left[ a,\;b \right]\]given by \[A=\int_{a}^{b}{|}f\left( x \right)-g\left( x \right)|dx\]
So, now we are given that \[{{y}^{2}}=x\], here we will isolate y and we get \[y=\pm \sqrt{x}\]. Next. Equation given here is \[y=x\]. So from that we can sat that our first function \[f\left( x \right)\]is \[y=\pm \sqrt{x}\]and the second function \[g\left( x \right)\] is \[y=x\]. Next to find the definite integral set up we have to find the integral limits, a and b. So, for that we have to find the intersections of the two curves \[y=\pm \sqrt{x}\] and \[y=x\].
So we will have to equate the two equations to get the x -coordinate of the intersection points, as shown below:
\[\begin{align}
  & \Rightarrow \pm \sqrt{x}=x \\
 & \Rightarrow x={{x}^{2}}\,\,\,\,\,\,\,\left[ Squaring\,\,both\,\,sides \right] \\
 & \Rightarrow x(x-1)=0 \\
 & \Rightarrow x=0,(x-1)=0 \\
 & \Rightarrow x=0,x=1 \\
\end{align}\]
So, here we will get two intersection points whose x-coordinates are\[x=0,x=1\] . So, for that we use the graphs, as follows:

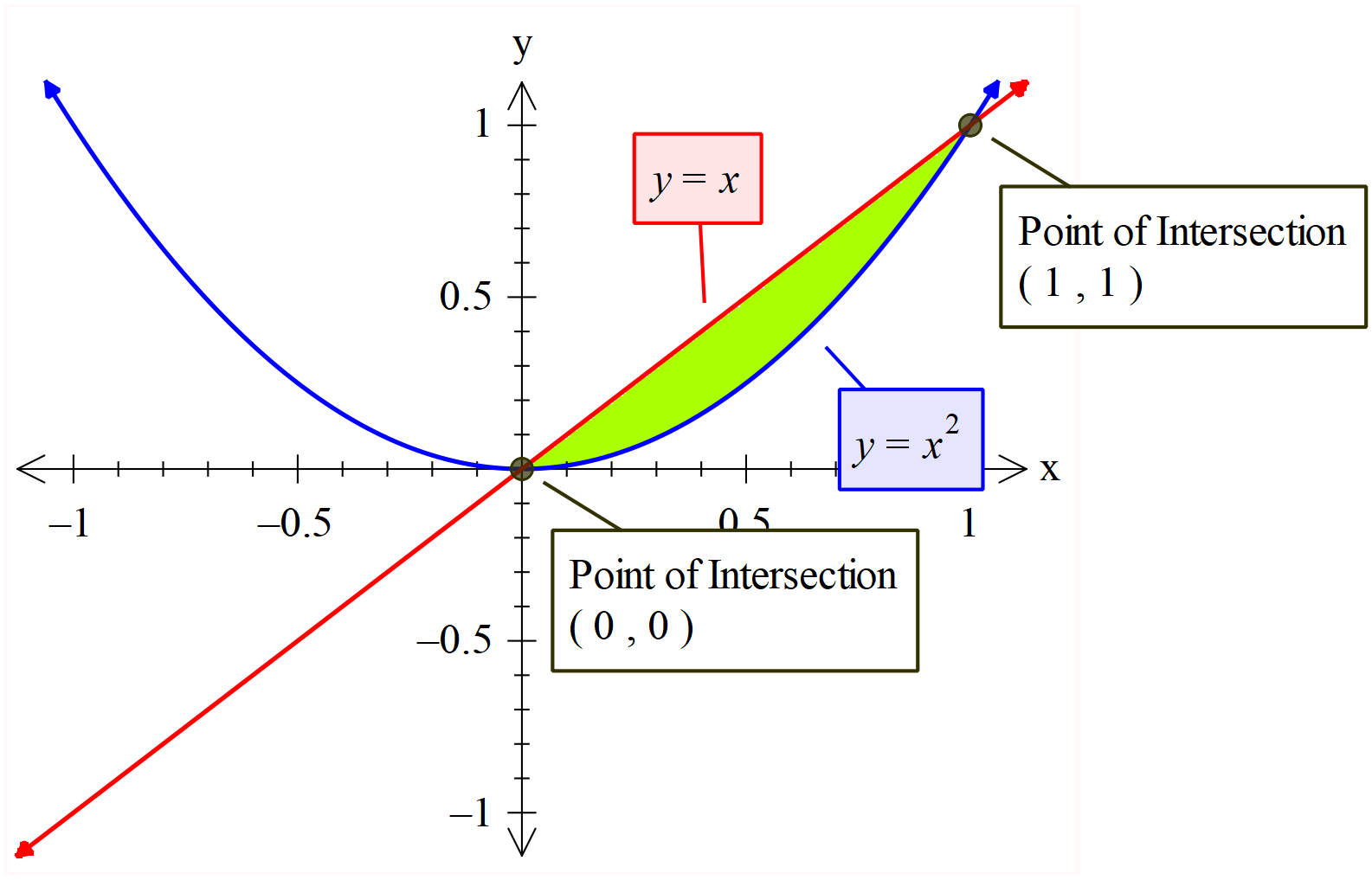
So here we have to find the area of the green region. So, the definite integral limits are \[a=0,\,\,b=1\].
Now, the area will be given by the definite integral:
\[\begin{align}
  & \Rightarrow A=\int_{a}^{b}{|}f\left( x \right)-g\left( x \right)|dx \\
 & \Rightarrow A=\int_{0}^{1}{\left| \sqrt{x}-x \right|}dx \\
 & \Rightarrow A=\int_{0}^{1}{\sqrt{x}}dx-\int_{0}^{1}{x}dx\,\,\,\,\,\,\,\,\because \left| \sqrt{x}-x \right|>0\,\,in\,\,[0,1] \\
\end{align}\]
Now, we will just have to solve the definite integral, to get the total area. So we will use the formula \[\int{{{x}^{a}}}dx=\dfrac{{{x}^{a+1}}}{a+1}+c,\;\quad \;a\ne -1\]
So, we will get the definite integral value, as follows:
\[\begin{align}
  & \Rightarrow A=\int_{0}^{1}{\sqrt{x}}dx-\int_{0}^{1}{x}dx\,\, \\
 & \Rightarrow A=\left[ \dfrac{{{x}^{\dfrac{1}{2}+1}}}{\dfrac{1}{2}+1} \right]_{0}^{1}-\left[ \dfrac{{{x}^{2}}}{2} \right]_{0}^{1} \\
 & \Rightarrow A=\left[ \dfrac{2}{3}{{x}^{\dfrac{3}{2}}} \right]_{0}^{1}-\left[ \dfrac{{{x}^{2}}}{2} \right]_{0}^{1} \\
 & \Rightarrow A=\dfrac{2}{3}-\dfrac{1}{2} \\
 & \Rightarrow A=\dfrac{1}{6} \\
\end{align}\]
So, this gives the final required area as \[\dfrac{1}{6}\]sq unit. Hence the correct answer is option D) \[\dfrac{1}{6}\]sq unit.

Note: It can be noted that we need to find the intersection points first. Also, it is not important to find the top and the bottom function in order to find the area enclosed between the functions \[{{y}^{2}}=x\]and \[y=x\]. Also, make sure there is no calculation error while solving the definite integrals.