Question

How do you find the area between \[f(x)={{x}^{2}}+2x+1\] and \[g(x)=3x+3\]?

Answer 1

Hint: From the given question we have been asked to find the area between two functions. For solving this question we will find the point of intersection of two functions. After finding it we will find the area of both functions and subtract the area of curve or function which is above among the both in the graph. So, we proceed with the solution as follows.

Complete step by step solution:
The point of intersection of these two functions are as follows.
We will equate both the functions and find the abscissa of the intersection point.
\[\Rightarrow {{x}^{2}}+2x+1=3x+3\]
\[\Rightarrow {{x}^{2}}+2x+1-3x-3=0\]
\[\Rightarrow {{x}^{2}}-x-2=0\]
Here we will add and subtract x on the left hand side of the equation.
\[\Rightarrow {{x}^{2}}-2x+x-2=0\]
\[\Rightarrow x\left( x-2 \right)+1\left( x-2 \right)=0\]
\[\Rightarrow \left( x-2 \right)\left( x+1 \right)=0\]
\[\Rightarrow x=2,-1\]
So, we will substitute this x points in one of the function and find the y points.
So, we get the equation as follows.
\[\Rightarrow y=3x+3\]
When we substitute x as \[2\] we get,
\[\Rightarrow y=3(2)+3\]
\[\Rightarrow y=9\]
When we substitute x as \[-1\] we get,
\[\Rightarrow y=3(-1)+3\]
\[\Rightarrow y=0\]
So, the points of intersection are \[(-1,0),(2,9)\].
The graph will be as follows.

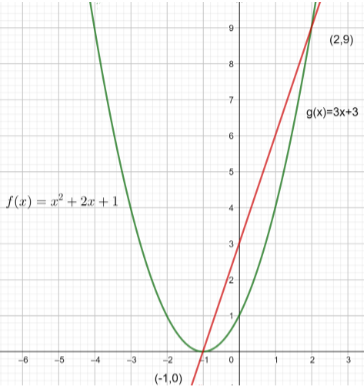
So, we have to find the area under the curve of \[g(x)\], then subtract the area under the curve \[f(x)\] because \[g(x)\] is above the function \[f(x)\] in the interval \[[-1,2]\].
We use integration for finding the area.
\[\Rightarrow \int\limits_{-1}^{2}{g(x)dx-\int\limits_{-1}^{2}{f(x)dx}}\]
\[\Rightarrow \int\limits_{-1}^{2}{(3x+3)dx-\int\limits_{-1}^{2}{({{x}^{2}}+2x+1)dx}}\]
Here we used the integration formulae which is \[\Rightarrow \int{{{x}^{n}}dx}=\dfrac{{{x}^{n+1}}}{n+1}\].
\[\Rightarrow \left[ \dfrac{3}{2}{{x}^{2}}+3x \right]_{-1}^{2}-\left[ \dfrac{1}{3}{{x}^{3}}+{{x}^{2}}+x \right]_{-1}^{2}\]
Now we remove the boundary by substituting them as follows.
\[\begin{align}
  & \Rightarrow \left[ \left( \dfrac{3}{2}\times {{2}^{2}}+3\times 2 \right)-\left( \dfrac{3}{2}\times {{(-1)}^{2}}+3\times (-1) \right) \right]- \\
 & \text{ }\left[ \left( \dfrac{1}{3}{{(2)}^{3}}+{{(2)}^{2}}+2 \right)-\left( \dfrac{1}{3}{{(-1)}^{3}}+{{(-1)}^{2}}+-1 \right) \right] \\
\end{align}\]
\[\Rightarrow \left[ \left( 6+6 \right)-\left( \dfrac{3}{2}-3 \right) \right]-\left[ \left( \dfrac{8}{3}+6 \right)-\left( \dfrac{-1}{3} \right) \right]\]
\[\Rightarrow 13.5-9\]
\[\Rightarrow 4.5\] square units

Note: Students must be very careful in doing the calculations. Students should know the concept of integration, areas and functions. Students should know the basic integration formulae like,
\[\Rightarrow \int{{{x}^{n}}dx}=\dfrac{{{x}^{n+1}}}{n+1}\]