Question

Find the area and perimeter of an isosceles right triangle, each of whose equal sides measures 10 cm. [Given: $\sqrt 2 = 1.41$]

Answer 1

Hint: The area of triangle is $\dfrac{1}{2} \times a \times b$. Since the triangle is an isosceles right-angle triangle therefore a=b=10cm. Perimeter of the triangle is the sum of the all sides of the triangle. For this we have to calculate the hypotenuse of all the triangles. Hypotenuse=$\sqrt {{{\left( {base} \right)}^2} + {{\left( {height} \right)}^2}} $

Complete step-by-step answer:

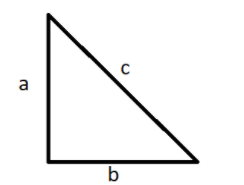
Area of triangle =$\dfrac{1}{2} \times a \times b$
Substituting a=b=10cm
Area of triangle =$\dfrac{1}{2} \times 10 \times 10 = 50c{m^2}$
Hypotenuse of triangle is $\sqrt {{{\left( {base} \right)}^2} + {{\left( {height} \right)}^2}} $ where base and height are equal to 10cm
Hypotenuse=$\sqrt {{{\left( {base} \right)}^2} + {{\left( {height} \right)}^2}} $
$ = \sqrt {{{10}^2} + {{10}^2}} = 10\sqrt 2 $cm
Given $\sqrt 2 = 1.41$
Hypotonus= 14.1cm
Now, perimeter of triangle is =sum of all sides of triangle
10+10+14.1=34.1cm
Therefore, area=$50c{m^2}$ and perimeter= 14.1cm.

Note: Alternative method to solve this ques
Hypotenuse of the given triangle is $\sqrt {{{\left( {base} \right)}^2} + {{\left( {height} \right)}^2}} $$ = \sqrt {{{10}^2} + {{10}^2}} = 10\sqrt 2 $cm
Sides of triangle is given

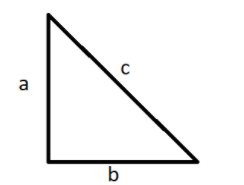
a=b=10cm, c=$10\sqrt 2 $cm semi perimeter is equal to s= $\dfrac{{10 + 10 + 10\sqrt 2 }}{2} = 5\left( {1 + \sqrt 2 } \right)cm$
Now, area=$\sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $
\[\sqrt {5(1 + \sqrt 2 )\left( {10 - 5 - 5\sqrt 2 } \right)\left( {10 - 5 - 5\sqrt 2 } \right)\left( {10\sqrt 2 - 5 - 5\sqrt 2 } \right)} \]=$50c{m^2}$