Question

How do you find the approximate area of an octagon given its diameter is 8 inches?

Answer 1

Hint: An octagon has eight sides and thus it can be divided into eight smaller triangles. These triangles would isosceles as two of its sides are equal. These equal sides would be half of the given diameter of the diameter. We shall calculate the angle subtended by any two sides of the octagon at its center. Thus, we shall find the area of one isosceles triangle and multiply it by eight to find the total area of the octagon.

Complete step-by-step answer:
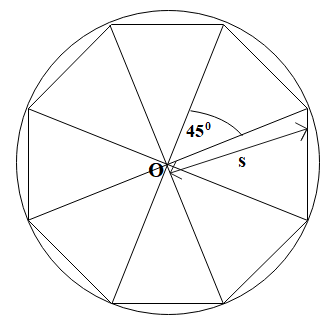
We know that the central angle of any geometric figure is ${{360}^{\circ }}$ when a complete revolution is taking place. We shall divide this angle, ${{360}^{\circ }}$ into eight equal parts to find the angle subtended by two sides of the octagon at its center, that is, the central angle $\left( \angle O \right)$ of each of the eight triangles.
$\Rightarrow \angle O=\dfrac{{{360}^{\circ }}}{8}$
$\Rightarrow \angle O={{45}^{\circ }}$
Given that the diameter of the octagon is 8 inches. Here, we shall imagine octagon to be inscribed inside a circle. In this case, the diameter of the octagon is twice the length of its one side $\left( s \right)$.
$\Rightarrow 2s=8$ inches
$\Rightarrow s=\dfrac{8}{2}$
$\Rightarrow s=4$inches
Thus, the side of the octagon is of 4 inches and the angle between them is ${{45}^{\circ }}$.

The area of an isosceles triangle is given as:
$A=\dfrac{1}{2}{{s}^{2}}\sin \theta $
Where, $\theta =$ the angle between the two equal sides $\left( s \right)$ of the isosceles triangle
$\Rightarrow A=\dfrac{1}{2}{{\left( 4 \right)}^{2}}\sin {{45}^{\circ }}$
We know that ${{4}^{2}}=16$ and $\sin {{45}^{\circ }}=\dfrac{1}{\sqrt{2}}$. Substituting these values, we get
$\Rightarrow A=\dfrac{1}{2}\left( 16 \right)\left( \dfrac{1}{\sqrt{2}} \right)$
$\Rightarrow A=\dfrac{8}{\sqrt{2}}$
$\Rightarrow A=4\sqrt{2}$square inches
Now, we shall multiply this area of one triangle into 8 to calculate the total area, ${{A}_{T}}$ of the octagon.
$\Rightarrow {{A}_{T}}=8\times A$
$\Rightarrow {{A}_{T}}=8\times 4\sqrt{2}$
$\Rightarrow {{A}_{T}}=32\sqrt{2}$
Since $\sqrt{2}=1.4142$,
 $\Rightarrow {{A}_{T}}=32\times 1.4142$
$\Rightarrow {{A}_{T}}=45.2544$ square inches
Therefore, the approximate area of an octagon given its diameter is 8 inches is $45.2544$square inches.

Note: While finding the areas of unconventional figures like an octagon, we must apply various other geometric properties after breaking the given figure into known conventional figures. The area of the circle circumscribing the octagon would also be approximately equal to the area of the octagon only.