Question

Find the angle which is $20{}^\circ $ more than its supplement
A.90
B.95
C.100
D.105

Answer 1

Hint: To answer this question, we use the concept of supplementary angles. Two angles are said to be supplementary if their sum is equal to $180{}^\circ .$ We assume that one angle is $\alpha $ and since the two angles are supplementary, the other angle is $180{}^\circ -\alpha .$ According to the question, we form an equation which shows that $\alpha $ is $20{}^\circ $ more than $180{}^\circ -\alpha .$ We then simplify for the value of $\alpha .$

Complete step by step solution:
We first explain what supplementary angles. Supplementary angles are two angles whose sum is equal to $180{}^\circ .$ Any two lines intersecting form angles with each other. The two angles at this common vertex represented by C can be depicted as in the figure below. Two line segments AB and CD intersect at a common vertex C. It forms two angles. Let us consider that the $\angle BCD=\alpha {}^\circ .$ Now we know that the sum of angles on a straight line add up to $180{}^\circ .$ Therefore, we calculate the $\angle ACD=180{}^\circ -\alpha {}^\circ .$

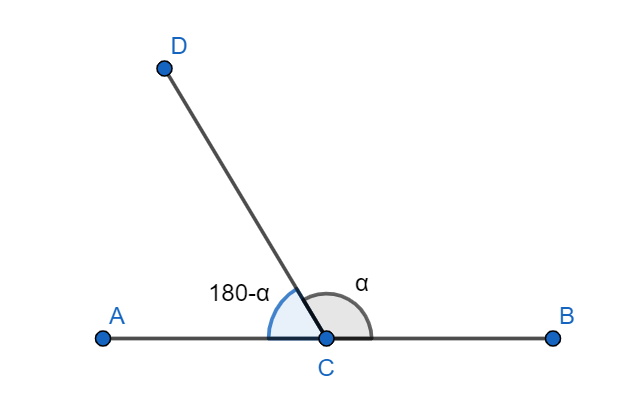
These two angles shown, are called supplementary angles since their sum is equal to $180{}^\circ .$
$\Rightarrow \alpha {}^\circ +180{}^\circ -\alpha {}^\circ =180{}^\circ $
Now for the given question, let us assume one of the angles to be $\alpha .$ Now since the two angles are supplementary, the other angle is $180{}^\circ -\alpha .$
It is given that the angle $\alpha $ is $20{}^\circ $ more than $180{}^\circ -\alpha .$ This can be written in equation form as,
$\Rightarrow \alpha =\left( 180{}^\circ -\alpha \right)+20{}^\circ $
Taking the $\alpha $ terms to one side and the constants to the other side,
$\Rightarrow \alpha +\alpha =180{}^\circ +20{}^\circ $
Adding the terms,
$\Rightarrow 2\alpha =200{}^\circ $
Dividing both sides by 2,
$\Rightarrow \dfrac{2}{2}\alpha =\dfrac{200{}^\circ }{2}$
Simplifying,
$\Rightarrow \alpha =100{}^\circ $
Hence, the correct option is B. This means that the angle which is $20{}^\circ $ more than its supplement is $100{}^\circ .$

Note: Students need to know the concept of supplementary angles in order to solve this question. It is to be notes that supplementary angles exist only for a pair of angles or in other words supplementary angles concept is applied only to two angles taken at a time. We cannot apply this concept to more than 2 angles taken at a time.