Question

Find the angle of depression if an observer 150 cm tall looks at the tip of his shadow which is \[150\sqrt{3}\]cm from his foot.

Answer 1

Hint: In this question, we first need to draw the figure with the given conditions so that it gives a clear picture of what we have to find. Then using the tangent formula which is given by \[\tan \theta =\dfrac{x}{y}\] on substituting the respective values and simplifying further gives the value of theta which will be the angle of depression.

Complete step by step answer:
ANGLE OF DEPRESSION:
The angle of depression is defined as the downward angle from the horizontal line of sight from the observer to some point of interest.
We require two quantities to get the angle of depression which are height and distance.
As we already know that the tangent formula is given by dividing the opposite side with the adjacent side.

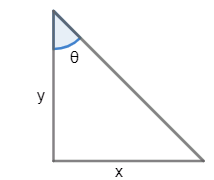
\[\tan \theta =\dfrac{x}{y}\]
Now, given that the distance of shadow from observer is \[150\sqrt{3}\] cm and height of observer is 150 cm
Let us now draw the diagram with the given conditions in the question,

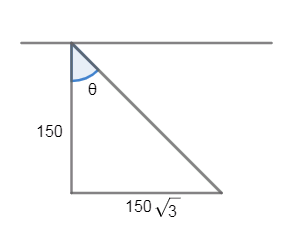
Now, on comparing the height and distance in the given question with the tangent formula we have
\[x=150\sqrt{3},y=150\]
Now, from the tangent formula we have
\[\Rightarrow \tan \theta =\dfrac{x}{y}\]
Now, on substituting the respective values we get,
\[\Rightarrow \tan \theta =\dfrac{150\sqrt{3}}{150}\]
Now, on cancelling the common terms we get,
\[\Rightarrow \tan \theta =\sqrt{3}\]
As we already know from the trigonometric ratios of some standard angles
\[\tan {{60}^{\circ }}=\sqrt{3}\]
Now, on further simplification we get,
\[\therefore \theta ={{60}^{\circ }}\]
Now, the angle of depression is given by
\[\Rightarrow {{90}^{\circ }}-\theta \]
Now, on substituting the respective value we get,
\[\Rightarrow {{90}^{\circ }}-{{60}^{\circ }}\]
Now, on further simplification we get,
\[\Rightarrow {{30}^{\circ }}\]
Hence, the angle of depression is \[{{30}^{\circ }}\].

Note:
Instead of using the tangent formula to get the value of theta we can also use cotangent formula and then substitute the respective values accordingly and simplify further which also gives the same result.
It is important to note that the angle depression is the angle made with the horizontal line but not the theta we found. So, we need to further subtract theta from 90 to get the angle of depression. If not done so then the result will be incorrect.