Question

Find the angle in the radian through which a pendulum swings if its length is 75 and the top describes an arc of length 21 cm.

Answer 1

Hint:We use the formula which connects the arc length to the central angle. Substitute the given values and find the value of \[\theta \]in radians.

Complete step-by-step answer:

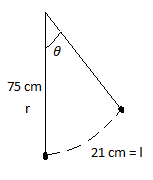
We have been given the length of pendulum swing = 75 cm.
The arc formed is of length = 21 cm.
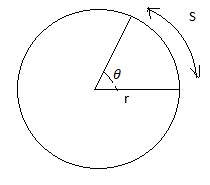
In the case of a circle, the formula which relates to the arc length of a radius r, to the central angle \[\theta \] is given as,
\[S=r\theta \]
Similarly in this case we can say that,
\[l=r\theta \]
where l is the length = 21 cm and r = 75 cm.
Thus substituting these values,
\[\begin{align}
  & 21=75\times \theta \\
 & \therefore \theta =\dfrac{21}{75}radians \\
 & \therefore \theta =\dfrac{7}{25}radians \\
\end{align}\]
Now we got the angle in which the pendulum swings = \[\dfrac{7}{25}radians\].

Note:Thus the angle in which a pendulum swings can be compared to the sector formed in the circle and thus we can establish the relation between the arc length and central angle \[\theta \].We have found the angle in radians. To convert it into degrees, multiply the angle with \[{}^{180}/{}_{\pi }\].