Question

Find the angle between the vectors whose direction cosines are proportional to 2, 3, -6 and 3, -4, 5.

Answer 1

Hint: The direction cosines of a line are cosines of the angles which the lines make with positive direction of coordinate axes. For any line, direction cosines will satisfy the ${l^2} + {m^2} + {n^2} = 1$
relation. Direction ratios are a set of three real numbers say a, b, c which are proportional to l, m, n means \[\dfrac{l}{a} = \dfrac{m}{b} = \dfrac{n}{c}\]. Any vector with direction ratio a, b, c can be represented in vector form as \[\overrightarrow A = a\widehat i + b\widehat j + c\widehat k\] . So, vector \[\overrightarrow A = 2\widehat i + 3\widehat j - 6\widehat k\] and \[\overrightarrow B = 3\widehat i - 4\widehat j + 5\widehat k\]. If the angle between two vectors is $\theta $ then, $\theta $ can be calculated by using $\cos \theta = \dfrac{{\overrightarrow A \cdot \overrightarrow B }}{{\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|}}$formula. Put the value, simplify the equation by taking dot product of vectors using $\overrightarrow A \cdot \overrightarrow B = ({a_1}\widehat i + {b_1}\widehat j + {c_1}\widehat k) \cdot ({a_2}\widehat i + {b_2}\widehat j + {c_2}\widehat k) = {a_1} \cdot {a_2} + {b_1} \cdot {b_2} + {c_1} \cdot {c_2}$) equation and mode of vectors using $\left| {\overrightarrow A } \right| = \sqrt {{a^2} + {b^2} + {c^2}} $ equation, we will obtain the angle between two vectors.

Complete step-by-step answer:
The direction cosines of a line are cosines of the angles which the lines make with positive direction of coordinate axes
Let’s take one line OL which is passing through origin O. Line OL makes an angle $\alpha $with X-axis, angle $\beta $ with Y-axis and angle $\gamma $ with Z-axis.

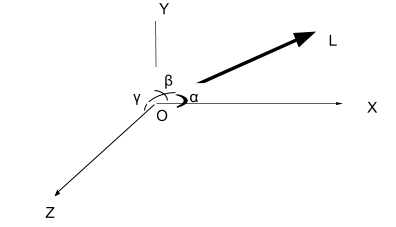
Now, the direction cosines of a line are given by, $l = \cos \alpha $, $m = \cos \beta $ and $n = \cos \gamma $
Direction cosines of any parallel lines will be the same.
Direction cosines for every line will satisfy ${l^2} + {m^2} + {n^2} = 1$ relation.
Now, direction ratios are simply a set of three real numbers a, b, c which are proportional to l, m, n.
So, \[\dfrac{l}{a} = \dfrac{m}{b} = \dfrac{n}{c}\]
Any vector with direction ratio a, b, c can be represented in vector form as \[\overrightarrow A = a\widehat i + b\widehat j + c\widehat k\],
Here for the first vector direction cosines are proportional to 2, 3, -6. So vector \[\overrightarrow A = 2\widehat i + 3\widehat j - 6\widehat k\] and for second vector direction cosines are proportional to 3, -4, 5. So, vector \[\overrightarrow B = 3\widehat i - 4\widehat j + 5\widehat k\].
If the angle between two vectors is $\theta $ then,
$\Rightarrow$$\cos \theta = \dfrac{{\overrightarrow A \cdot \overrightarrow B }}{{\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|}}$
Now use the formula for dot product of vectors,
$\overrightarrow A \cdot \overrightarrow B = ({a_1}\widehat i + {b_1}\widehat j + {c_1}\widehat k) \cdot ({a_2}\widehat i + {b_2}\widehat j + {c_2}\widehat k) = {a_1} \cdot {a_2} + {b_1} \cdot {b_2} + {c_1} \cdot {c_2}$
Putting the value of vector \[\overrightarrow A = 2\widehat i + 3\widehat j - 6\widehat k\] and \[\overrightarrow B = 3\widehat i - 4\widehat j + 5\widehat k\]
$\overrightarrow A \cdot \overrightarrow B = (2\widehat i + 3\widehat j - 6\widehat k) \cdot (3\widehat i - 4\widehat j + 5\widehat k)$
Simplifying, $\overrightarrow A \cdot \overrightarrow B = (2) \cdot (3) + (3) \cdot ( - 4) + ( - 6) \cdot (5)$
$\Rightarrow$$\overrightarrow A \cdot \overrightarrow B = 6 - 12 - 30$
So, $\overrightarrow A \cdot \overrightarrow B = - 36$
Now use formula for modulus of vector, $\left| {\overrightarrow A } \right| = \sqrt {{a^2} + {b^2} + {c^2}} $
For \[\overrightarrow A = 2\widehat i + 3\widehat j - 6\widehat k\] put value of ${a_1} = 2$, ${b_1} = 3$ and ${c_1} = - 6$
So $\left| {\overrightarrow A } \right| = \sqrt {{{(2)}^2} + {{(3)}^2} + {{( - 6)}^2}} $
Simplifying, $\left| {\overrightarrow A } \right| = \sqrt {4 + 9 + 36} $
$\Rightarrow$$\left| {\overrightarrow A } \right| = \sqrt {49} $
So, $\left| {\overrightarrow A } \right| = 7$
Similarly using same equation for vector, \[\overrightarrow B = 3\widehat i - 4\widehat j + 5\widehat k\]
For \[\overrightarrow B = 3\widehat i - 4\widehat j + 5\widehat k\] put value of ${a_1} = 3$, ${b_1} = - 4$ and ${c_1} = 5$
So, $\left| {\overrightarrow B } \right| = \sqrt {{{(3)}^2} + {{( - 4)}^2} + {{(5)}^2}} $
Simplifying, \[\left| {\overrightarrow B } \right| = \sqrt {9 + 16 + 25} \]
$\Rightarrow$$\left| {\overrightarrow B } \right| = \sqrt {50} $
So, $\left| {\overrightarrow B } \right| = \sqrt {25 \times 2} = 5\sqrt 2 $
Now, putting all the values in $\cos \theta = \dfrac{{\overrightarrow A \cdot \overrightarrow B }}{{\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|}}$ equation
So, $\cos \theta = \dfrac{{ - 36}}{{7 \cdot 5\sqrt 2 }}$
$\Rightarrow$$\cos \theta = \dfrac{{ - 36}}{{35\sqrt 2 }}$
Further simplifying, \[\cos \theta = \dfrac{{ - 18 \cdot 2}}{{35\sqrt 2 }} = \dfrac{{ - 18 \cdot \sqrt 2 \cdot \sqrt 2 }}{{35\sqrt 2 }} = \dfrac{{ - 18 \cdot \sqrt 2 }}{{35}}\]
Taking ${\cos ^{ - 1}}$on both side of equation,
$\Rightarrow$\[\theta = {\cos ^{ - 1}}(\dfrac{{ - 18 \cdot \sqrt 2 }}{{35}})\]

So, angle between the vectors whose direction cosines are proportional to 2, 3, -6 and 3, -4, 5 is given by \[\theta = {\cos ^{ - 1}}(\dfrac{{ - 18 \cdot \sqrt 2 }}{{35}})\].

Note: For any line there must be unique direction cosines. As direction ratios are just a set of any three real numbers which are proportional to direction cosines, there are infinitely many sets of direction ratios. If the direction ratios of a line a, b, c are given then using the following equation we can find the direction cosines.
$l = \pm \dfrac{a}{{\sqrt {{a^2} + {b^2} + {c^2}} }}$, $m = \pm \dfrac{b}{{\sqrt {{a^2} + {b^2} + {c^2}} }}$ and $n = \pm \dfrac{c}{{\sqrt {{a^2} + {b^2} + {c^2}} }}$.