Question

How do you find the angle between the vectors \[u=3\overset{\wedge }{\mathop{i}}\,+4\overset{\wedge }{\mathop{j}}\,\] and \[v=-2\overset{\wedge }{\mathop{j}}\,\]?

Answer 1

Hint: Take the dot product of the two vectors by assuming that the angle between them is $\theta $. To find \[\overset{\to }{\mathop{u}}\,.\overset{\to }{\mathop{v}}\,\], that is the dot product of vectors u and v, multiply the coefficients of \[\overset{\wedge }{\mathop{i}}\,,\overset{\wedge }{\mathop{j}}\,\] of vector u with the corresponding coefficients of \[\overset{\wedge }{\mathop{i}}\,,\overset{\wedge }{\mathop{j}}\,\] of vector v. Use the fact that the dot product of two perpendicular vectors is 0, so \[\overset{\wedge }{\mathop{i}}\,.\overset{\wedge }{\mathop{j}}\,=\overset{\wedge }{\mathop{j}}\,.\overset{\wedge }{\mathop{i}}\,=0\], to simplify the answer. Find the magnitude of the vector given as \[\overset{\to }{\mathop{a}}\,=x\overset{\wedge }{\mathop{i}}\,+y\overset{\wedge }{\mathop{j}}\,\] by using the formula: $a=\sqrt{{{x}^{2}}+{{y}^{2}}}$ and hence find the value of $\theta $.

Complete step by step solution:
Here, we have been provided with two vectors, \[u=3\overset{\wedge }{\mathop{i}}\,+4\overset{\wedge }{\mathop{j}}\,\] and \[v=-2\overset{\wedge }{\mathop{j}}\,\], and we are asked to find the angle between the two vectors. Here, we will use the formula of the dot product of two vectors.
Now, the dot product of two vectors is defined as the product of the magnitude of two vectors and the cosine of the angle between them. For example: - let us consider two vectors, \[\overset{\to }{\mathop{x}}\,\] and \[\overset{\to }{\mathop{y}}\,\] and the angle between them is \[\theta \]. So, the dot product of these vectors is given as: -

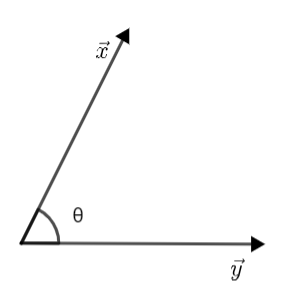
\[\Rightarrow \overrightarrow{x}.\overrightarrow{y}=xy\cos \theta \]
Here, x denotes the magnitude of \[\overrightarrow{x}\] and similarly y denotes the magnitude of \[\overrightarrow{y}\]. Now, one thing you may note is that when the two vectors are perpendicular, i.e., \[\theta ={{90}^{\circ }}\], then the dot product of two vectors will become zero. This is because \[\cos {{90}^{\circ }}=0\].
Now, we know that \[\overset{\wedge }{\mathop{i}}\,,\overset{\wedge }{\mathop{j}}\,\] are perpendicular to each other as they represent unit vectors along the x, y axis respectively. So, we have,
\[\Rightarrow \overset{\wedge }{\mathop{i}}\,.\overset{\wedge }{\mathop{j}}\,=\overset{\wedge }{\mathop{j}}\,.\overset{\wedge }{\mathop{i}}\,=0\]
That means we have to take the product of \[\overset{\wedge }{\mathop{i}}\,,\overset{\wedge }{\mathop{j}}\,\] of one vector with the corresponding \[\overset{\wedge }{\mathop{i}}\,,\overset{\wedge }{\mathop{j}}\,\] of the second vector. Here, \[\overset{\wedge }{\mathop{i}}\,.\overset{\wedge }{\mathop{i}}\,=\overset{\wedge }{\mathop{j}}\,.\overset{\wedge }{\mathop{j}}\,=1\] because in these two cases \[\theta ={{0}^{\circ }}\] and we know that \[\cos {{0}^{\circ }}=1\].
Let us come to the question, considering the dot product of vectors u and v by assuming that the angle between them is $\theta $, we get,
\[\begin{align}
  & \Rightarrow \overset{\to }{\mathop{u}}\,.\overset{\to }{\mathop{v}}\,=\left( 3\overset{\wedge }{\mathop{i}}\,+4\overset{\wedge }{\mathop{j}}\, \right).\left( -2\overset{\wedge }{\mathop{j}}\, \right) \\
 & \Rightarrow uv\cos \theta =\left( 4\times \left( -2 \right) \right) \\
 & \Rightarrow uv\cos \theta =-8 \\
\end{align}\]
Using the formula for finding the magnitude of \[\overset{\to }{\mathop{a}}\,=x\overset{\wedge }{\mathop{i}}\,+y\overset{\wedge }{\mathop{j}}\,\] given as: $a=\sqrt{{{x}^{2}}+{{y}^{2}}}$, we get,
\[\begin{align}
  & \Rightarrow \sqrt{{{3}^{2}}+{{4}^{2}}}\times \sqrt{{{\left( -2 \right)}^{2}}}\times \cos \theta =-8 \\
 & \Rightarrow 5\times \sqrt{4}\times \cos \theta =-8 \\
 & \Rightarrow 5\times 2\times \cos \theta =-8 \\
 & \Rightarrow 10\cos \theta =-8 \\
 & \Rightarrow \cos \theta =\dfrac{-8}{10} \\
 & \Rightarrow \cos \theta =\dfrac{-4}{5} \\
 & \Rightarrow \theta ={{\cos }^{-1}}\left( \dfrac{-4}{5} \right) \\
\end{align}\]
Hence, the above relation is required answer

Note: You can remember that the value of cosine function is \[\dfrac{4}{5}\] when the value of $\theta $ is ${{37}^{\circ }}$ but in the above relation of $\cos \theta $ we have the its value equal to \[\dfrac{-4}{5}\] which is negative, that means $\theta $ will lie in second quadrant due to the limitation ${{0}^{\circ }}\le \theta \le {{180}^{\circ }}$ in vectors. Therefore, the actual value of $\theta $ will be $\left( {{180}^{\circ }}-{{37}^{\circ }} \right)={{143}^{\circ }}$. We can also solve this question by using the cross product of two vectors.