Question

Find the angle between the medians of the legs of an isosceles right triangle.

Answer 1

Hint: We will make an isosceles right triangle and right angle at point $ B $ . Further, we will calculate the sides of the triangle by using Pythagoras theorem. Thereafter, we will find the required angle with the help of a centroid in a triangle.

Complete step-by-step answer:

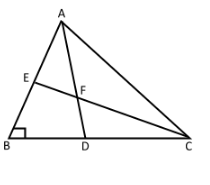
Let $ \Delta ABC $ be an isosceles right triangle and right angle at point $ B $ .
Let $ AD $ be the median of side \[BC\]and $ CE $ is the median of side $ AB $ .
As we know that $ \angle B = {90^o} $ and in the isosceles triangle two sides are equal in length.
Let $ AB = BC = x $
Now, we will use Pythagoras theorem
 $\Rightarrow {(hypotenuse)^2} = {(base)^2} + {(perpendicular)^2} $
 $ {(AC)^2} = {(BC)^2} + {(AB)^2} $
 $ {(AC)^2} = {(x)^2} + {(x)^2} $
 $ {(AC)^2} = {x^2} + {x^2} $
 $ A{C^2} = 2{x^2} $
 $ AC = \sqrt {2{x^2}} $
 $ AC = \sqrt 2 x $
Since, the triangle is an isosceles triangle
 $ \therefore AB = BC $
 $ \Rightarrow \angle BAC = \angle BCA $ $ (\because $ Angle opposite to equal sides are equal)
As $ AD $ is median of $ BC, $
 $ \Rightarrow BD = DC = \dfrac{{BC}}{2} = \dfrac{x}{2} $
And $ CE $ is median of $ AB $ ,
 $ \Rightarrow AE = EB = \dfrac{x}{2} = \dfrac{{AB}}{2} $
Now, in $ \Delta ABD, $
 $ AB = x,\,BD = \dfrac{x}{2} $
By using Pythagoras, we will have
 $\Rightarrow {(hypotenuse)^2} = {(base)^2} + {(perpendicular)^2} $
 $ {(AD)^2} = {(BD)^2} + {(AB)^2} $
 $ {(AD)^2} = {\left( {\dfrac{x}{2}} \right)^2} + {(x)^2} $
\[{(AD)^2} = \dfrac{{{x^2}}}{4} + \dfrac{{{x^2}}}{1}\]
We will take LCM of $ 1,4 = 4 $ , so
 $ {(AD)^2} = \dfrac{{{x^2} + 4.{x^2}}}{4} $
 $ A{D^2} = \dfrac{{5{x^2}}}{4} $
 $ AD = \sqrt {\dfrac{{5{x^2}}}{4}} $
 $ AD = \dfrac{{\sqrt 5 x}}{2} $
Now, in $ \Delta BCE,BE = \dfrac{x}{2},BC = x $
Again by using Pythagoras theorem, we have
 $ {(hypotenuse)^2} = {(base)^2} + {(perpendicular)^2} $
 $ {(CE)^2} = {(BC)^2} + {(BE)^2} $
 $ {(CE)^2} = {(x)^2} + \dfrac{{{x^2}}}{4} $
\[{(CE)^2} = \dfrac{{4{x^2} + 1{x^{_2^{}}}}}{4}\]
 $ {(CE)^2} = \dfrac{{5{x^2}}}{4} $
 $ CE = \dfrac{{\sqrt {5{x^2}} }}{4} $
 $ CE = \dfrac{{\sqrt 5 x}}{2} $
As $ G $ is centroid, it divides each median in the ratio $ 2:1 $
 $ \Rightarrow AF = FD = 2F = \dfrac{2}{3} \times D $
 $ \Rightarrow AF = FD = \dfrac{{\sqrt 5 }}{3}x $
In $ \Delta AFC, $ $ AF = FC = \dfrac{{\sqrt 5 }}{3}x $
 $ AC = \sqrt 2 x $
So, $ \cos (\angle AFC) = \dfrac{{{{(AF)}^2} + {{(FC)}^2} - {{(AC)}^2}}}{{2(AF) \times (FC)}} $
\[\cos (\angle AFC) = \dfrac{{{{\left( {\dfrac{{\sqrt 5 }}{3}x} \right)}^2} + {{\left( {\dfrac{{\sqrt 5 }}{3}x} \right)}^2} - {{\left( {\sqrt 2 x} \right)}^2}}}{{2 \times \dfrac{{\sqrt 5 }}{3}x \times \dfrac{{\sqrt 5 }}{3}x}}\]
$ \cos (\angle AFC) = \dfrac{{\dfrac{5}{9}{x^2} + \dfrac{5}{9}{x^2} - 2{x^2}}}{{2 \times \dfrac{5}{9}{x^2}}} $
Take LCM $ 9 $ in the numerator, we have
$ \cos (\angle AFC) = \dfrac{{\dfrac{{5{x^2} + 5{x^2} - 18{x^2}}}{9}}}{{2 \times \dfrac{5}{9}{x^2}}} $
 $ \cos (\angle AFC) = \dfrac{{\dfrac{{10{x^2} - 18{x^2}}}{9}}}{{\dfrac{{10}}{9}{x^2}}} $
 $ \cos (\angle AFC) = \dfrac{{\dfrac{{ - 8{x^2}}}{9}}}{{\dfrac{{10}}{9}{x^2}}} $
 $ \cos (\angle AFC) = \dfrac{{ - 8}}{9}{x^2} \times \dfrac{9}{{10}} \times \dfrac{1}{{{x^2}}} $
 $ = \dfrac{{ - 4}}{5} $
So, $ \cos (\pi - \angle AFC) = \dfrac{4}{5} $
 $ \Rightarrow \cos (\angle AFC) = \dfrac{4}{5} $
 $ \Rightarrow \angle AFC = {\cos ^{ - 1}}\left( {\dfrac{4}{5}} \right) \approx 36.87 $

Note: Students must know that the centroid divides the medians in the ratio $ 2:1 $ in a triangle, where medians intersect each other. This is the very important point to be remembered about the centroid of the triangle.