Question

Find the angle between the lines $x + y + 1 = 0$ and $x = 5$

Answer 1

Hint: We will begin by calculating slope of the lines using the formula $ - \dfrac{b}{a}$, when the equation of line is $ax + by + c = 0$. Then, we will find the angle $\theta $ between the lines by plotting the graph of the lines and using the condition $m = \tan \theta $, where $m$ is the slope and $\theta $ is the angle between the line and the $x$ axis. We will use various properties of angles and sum of triangles to find required angles.

Complete step-by-step answer:
First of all, we will find the slope of the lines $x + y + 1 = 0$ and $x = 5$.
We know that the slope of any line $ax + by + c = 0$ is given as $ - \dfrac{b}{a}$
Here the slope of line $x + y + 1 = 0$ will be $\dfrac{{ - 1}}{1} = - 1$
And the slope of the line $x = 5$ is $\dfrac{1}{0}$,
Since, the slope is undefined.
We will plot the graph of the equations and then find the required angle.

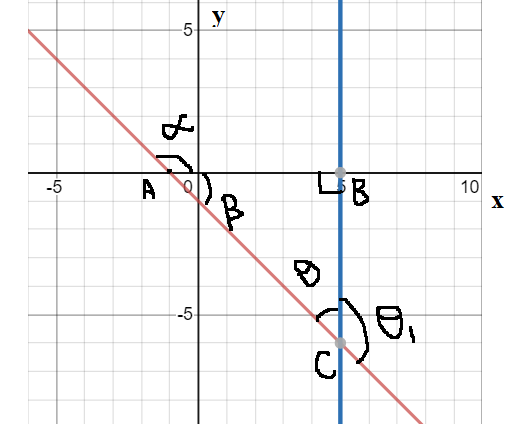
We have to find the angle $\theta $, that is the line $x + y + 1 = 0$ and $x = 5$.
Here, the $\alpha $ is the angle between the line and the\[x\]axis.
Then, \[\tan \alpha = m\] , where $m$ is the slope of the line.
Therefore, $\tan \alpha = - 1$
Then, $\alpha = \dfrac{{3\pi }}{4}$
Also, we know that angles on the same line are supplementary to each other.
Hence, $\alpha + \beta = \pi $
On substituting the value of $\alpha = \dfrac{{3\pi }}{4}$ in the above equation, we will get,
$
  \dfrac{{3\pi }}{4} + \beta = \pi \\
   \Rightarrow \beta = \dfrac{\pi }{4} \\
$
And the sum of all angles of triangle ABC should be ${180^ \circ }$ which is $\pi $.
Hence,
$
  \dfrac{\pi }{2} + \beta + \theta = \pi \\
   \Rightarrow \dfrac{\pi }{2} + \dfrac{\pi }{4} + \theta = \pi \\
   \Rightarrow \theta = \pi - \left( {\dfrac{{3\pi }}{4}} \right) \\
   \Rightarrow \theta = \dfrac{\pi }{4} \\
$
Hence, the angle between the lines $x + y + 1 = 0$ and $x = 5$ is $\dfrac{\pi }{4}$.
The angle ${\theta _1}$ will also be the angle between the given lines.
And $\theta $ and ${\theta _1}$ are supplementary angles, therefore,
$
  \theta + {\theta _1} = \pi \\
   \Rightarrow \dfrac{\pi }{4} + {\theta _1} = \pi \\
   \Rightarrow {\theta _1} = \dfrac{{3\pi }}{4} \\
$
Thus, the angle between the lines $x + y + 1 = 0$ and $x = 5$ is $\dfrac{\pi }{4}$ or $\dfrac{{3\pi }}{4}$.

Note: The slope of the line which is parallel to the\[y\] axis is not defined and the slope of the line which is parallel to $x$ axis is 0. Whenever two lines intersect, four angles are formed out of which two pairs are always equal. The value of angles is such that they form a supplementary pair.

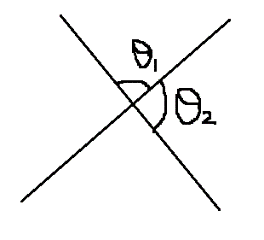
${\theta _1} + {\theta _2} = \pi $
Angle $\theta $ between the lines using the formula, $\tan \theta = \left| {\dfrac{{{m_1} - {m_2}}}{{1 + {m_1}{m_2}}}} \right|$, where ${m_1}$ and ${m_2}$ are slopes of two lines.