Question

Find the angle between minute and hour hand at 12 o’ clock.
A.\[{{0}^{\circ }}\]
B\[{{90}^{\circ }}\]
C.\[{{120}^{\circ }}\]
D.\[{{160}^{\circ }}\]

Answer 1

Hint: A clock has a shape of the circle made up of \[{{360}^{\circ }}\], as a clock has 12 hours, each hour will draw an angle measure of \[{{30}^{\circ }}\]. By drawing a clocking diagram in this case minute hand and hour hand are overlapping each other that means there is no angle between them hence, it is \[{{0}^{\circ }}\]. In this way we have to approach the problem.

Complete step-by-step answer:
A clock diagram of 12 o’clock is given below:

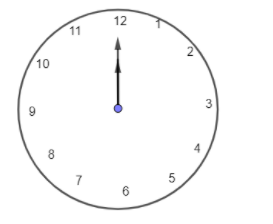
Our task is to find the angle between minute hand hour hand at 12 o’ clock.
These types of problems are clock angle problems where we must find the angle between the hands of an analog clock that shows us time 12 sections, as there are 12 numbers on the clock that represents the hours. Keeping this in mind we can say that each number represents a definite angle.
As it is divided into 12 equal parts, the measure of the angle between each number is given as:
\[\dfrac{360}{12}=30\]
Similarly, we can also measure angle between minute hand and hour hand per minute is given as \[\dfrac{360}{60}=6\]
This is general information about clocks now, we come to the question.
In this question the timing is given as 12 o’clock.
If you see in the above clock diagram, minute and hour hand both are at 12 o’ clock and both are overlapping to each other. That means minute hand and hour hand are the same lines.
Therefore, the angle between them is \[{{0}^{\circ }}\] or we can say that anyone has completed a complete circle.
Therefore, the angle between the hands of a clock at 12 o’clock is \[{{0}^{\circ }}\].
So, the correct option is “option A”.
So, the correct answer is “Option A”.

Note: We can illustrate by representing the clock diagram and timing is 12 o’clock and observe the minute hand and hour hand make a straight line so we can directly say that angle is \[{{0}^{\circ }}\]similarly if the question is asked about 6 o’clock then also illustrate a diagram for that then you can directly say that angle between hands is \[{{180}^{\circ }}\]. Formula \[\theta ={{\theta }_{H}}-{{\theta }_{M}}\] where \[{{\theta }_{H}}\] be the angle hour hand makes when it moves from 12o’clock and \[{{\theta }_{M}}\] be the angle hour hand makes when it moves from 12o’clock.