Question

How do you find the angle $\alpha$ such that the angle lies in quadrant $IV$ and $\tan \alpha =-0.7265$ ?

Answer 1

Hint: We have to find the value of $\alpha$ by using the tangent function. We start to solve the problem by isolating the value of $\alpha$ to find the value of the angle $\alpha$ that lies in $IV\;$ with the help of trigonometric formulae.

Complete step by step solution:
We are given the value of $\tan \alpha$ and need to find out the value of an angle $\alpha$ . We need to isolate $\alpha$ to find its value.
Tangent is the trigonometric function of any specified angle that is used in the context of a right angle.
It is usually defined as the ratio of the length of the side opposite to an angle to the length of the side adjacent to an angle of the right-angle triangle.
$\Rightarrow \tan \alpha =\dfrac{\text{length of the side opposite to }\alpha }{\text{length of the side adjacent to }\alpha }$
In the given right-angled triangle,

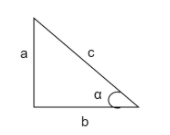
The value of $\tan \alpha$ is given by the ratio of opposite side to an angle $\alpha$ to the adjacent side to an angle $\alpha$
Adjacent side to angle $\alpha$ $=$ b
Opposite side to angle $\alpha$ $=$ a
Hypotenuse $=$ c
$\Rightarrow \tan \alpha =\dfrac{a}{b}$
According to the question,
The given angle lies in $IV$ quadrant.
In $IV$ quadrant, the values of tan are negative.
As per the question,
$\Rightarrow \tan \alpha =-0.7265$
We need to isolate the angle $\alpha$ to find its value.
tan function on shifting to the right-hand side of the equation becomes tan inverse of arctan function denoted by ${{\tan }^{-1}}$
arctan and tan functions are inverses of each other.
Shifting the tan function to the other side of the equation, we get,
$\Rightarrow \alpha ={{\tan }^{-1}}\left( -0.7265 \right)$
From trigonometry,
The value of ${{\tan }^{-1}}\left( -\alpha \right)$ is given by
$\Rightarrow {{\tan }^{-1}}\left( -\alpha \right)=-\tan \alpha$
Substituting the same, we get,
$\Rightarrow \alpha =-{{\tan }^{-1}}\left( 0.7265 \right)$
Using the tan inverse calculator, we get,
$\therefore \alpha =-35.99{}^\circ$

Note: We need to know the relation between tan and inverse tan functions to solve this problem easily. The value of the tan function is negative in $IV$ quadrant and positive in $I$ and $III$ quadrant. The value of $\alpha$ can be cross checked by putting the value in the equation $\tan \alpha =-0.7265$.
LHS:
$\Rightarrow \tan \alpha$
$\Rightarrow \tan \left( -35.99 \right)$
$\Rightarrow -0.7265$
RHS:
$\Rightarrow -0.7265$
LHS=RHS
The result attained is correct.