Question

How do you find the amplitude, period, vertical and phase shift, and graph \[y=2\cot (3\theta +135)-6\]?

Answer 1

Hint: To find any values, firstly we need to compare the given equation with the standard equation \[y=a\cot (bx-c)+d\] and calculate the values required. The period for tangent and cotangent functions for the standard form is \[\pi \]. Period depends on the coefficient of x in the general equation \[y=a\cot (bx-c)+d\].

Complete step by step answer:
As per the given question, we need to find the amplitude, period, vertical, and phase shift of the given trigonometric function, and then we have to graph the function. Now, we compare the given equation with the standard form of the equation.
\[\Rightarrow y=a\cot (bx-c)+d\]
\[\Rightarrow y=2\cot (3\theta +135)-6\]
On comparing, the values are \[a=3,b=3,c=-135,d=-6\].
The amplitude will be a which is equal to 3.
The period is the duration of time for one cycle in a repeating event. The period of the function of this form is \[\dfrac{\pi }{|b|}\] .
\[\therefore \] The period of the given function will be \[\dfrac{\pi }{|3|}=\dfrac{\pi }{3}\].
The phase shift of the function in this form is \[\dfrac{c}{b}\]. That is, the phase shift of the given function will be \[\dfrac{-135}{3}=-45\].
Since the phase shift is negative, it is directed towards the left of the graph.
The vertical shift of the function in this form is \[d\]. So, the vertical shift of the given function is \[-6\].
The following graph shows the graph of the given function.

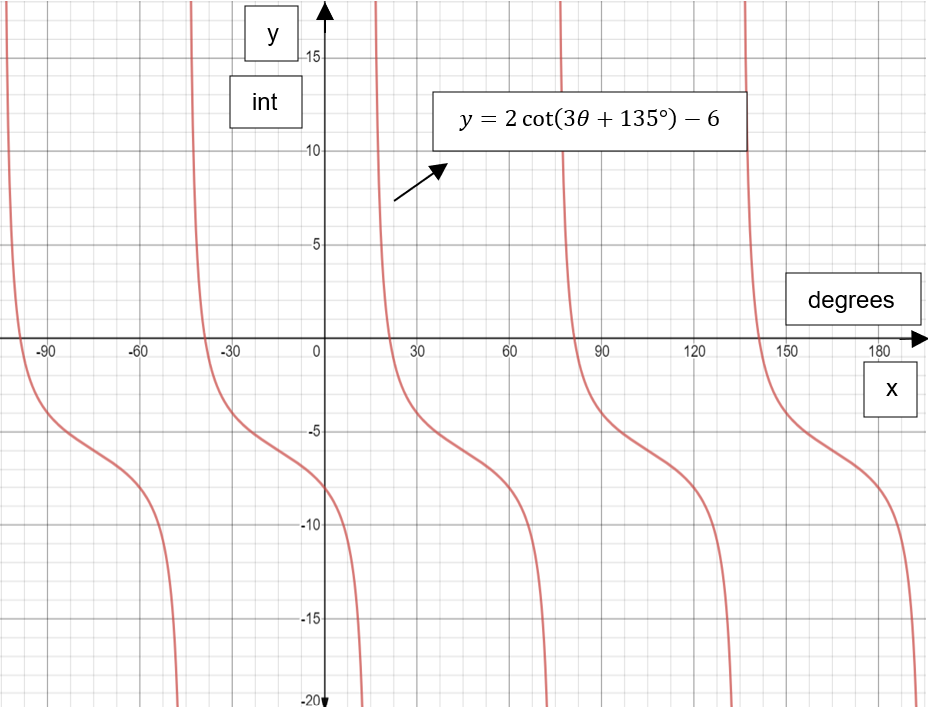
Note:
 The above method is the easiest method to find the given values. while plotting the graph make sure whether we use radians or degrees. Plot the points wisely such that they can be easily calculated from the equation. While comparing the given equation with the standard equation check the coefficients in order to get the correct solution.