Question

Find the amount of water displaced by a solid spherical ball of diameter:
i)28 cm
ii) 0.21m

Answer 1

Hint: We can find the amount of water displaced by anybody by calculating its volume as the water that can be contained in any vessel is equal to what can be displaced.
Volume of sphere =$4/3\pi {r^3}$

Complete step-by-step answer:

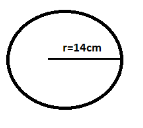
i.Diameter= 28cm
Radius , $r = 28/2 = 14$cm (As diameter= 2 radius , ∴Radius= Diameter/2)
We Know, Amount of water displaced= Volume of sphere
And, Volume of sphere =$4/3\pi {r^3}$
Substituting value of r, we get:
\[4/3\pi {r^3} = (4/3)\pi {(14)^3}\]
 \[
   = (4/3)(22/7) \times 14 \times 14 \times 14 \\
   = 34496/3 \\
 \]
\[ = 11498.66\]cm³

ii.Diameter= 0.21m

Radius , \[\]$r = 0.21/2 = 0.105$m (As diameter= 2 radius , ∴Radius= Diameter/2)
We Know, Amount of water displaced= Volume of sphere
And, Volume of sphere =$4/3\pi {r^3}$
Substituting value of r, we get:
\[4/3\pi {r^3} = (4/3)\pi {(0.105)^3}\]
\[
   = (4/3)(22/7) \times 0.105 \times 0.105 \times 0.105 \\
   = (4/3) \times (22/7) \times (105/1000) \times (105/1000) \times (105/1000) \\
   = 4851000/1000000000 \\
 \]
\[ = .004851\]m³

Therefore, Amount of water displaced by a solid spherical ball is 11498.66cm³, when radius is 28cm and 0.004851m³ when radius is 0.21m

Note: Be careful about the unit of radius( like cm will be provide volume in cm³)
Remember that the amount of water displaced by any body will always be equal to its volume. In sphere, all the points on the surface are equidistant from the centre and has constant width and circumference