Question

Find the acceleration of $ M $

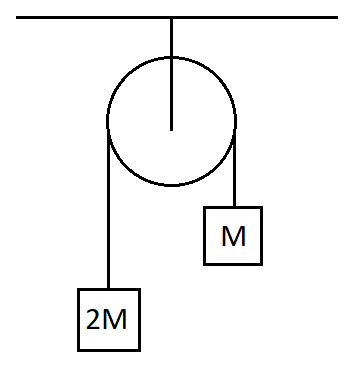
Answer 1

Hint
To solve this problem we need to first draw the free body diagram of the 2 masses considering the pulley to be weightless. Then from the equation of the 2 masses from the free body diagram, we can equate the tension of the string in the 2 cases and hence derive the acceleration.

Formula Used: In this solution we will be using the following formula,
 $ {F_{net}} = Ma $
where $ {F_{net}} $ is the net force acting on the body,
 $ M $ is the mass of the body and $ a $ is the acceleration of the body.

Complete step by step answer
To find the acceleration of the 2 masses we first need to draw the free body diagram of the 2 bodies to determine the direction in which the forces are acting.

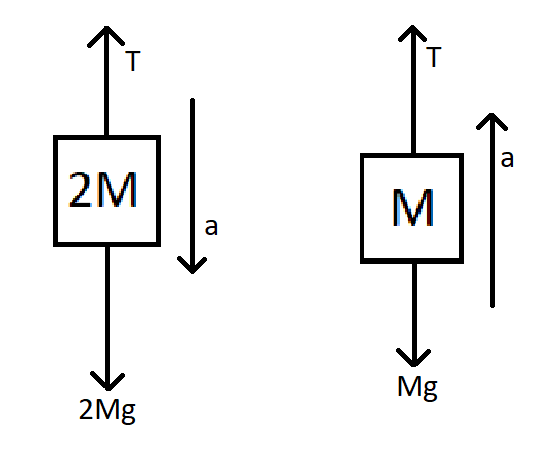
From the free body diagram of the mass $ 2M $ we see that the forces acting on it are due to the tension in the string in the upward direction and the weight of the body acting in the downward direction. There is net force acting on the body due to which the acceleration of the body is in the downward direction. Therefore we can write, $ {F_{net}} = 2Ma $
Now the net force will be the difference in the tension and the weight of the body. Hence,
 $ 2Mg - T = 2Ma $
From here we can write,
 $ T = 2Mg - 2Ma $
Taking $ 2M $ common in the RHS,
 $ T = 2M\left( {g - a} \right) $
Now from the free body diagram of the mass $ M $ we can see that is a similar way, 2 forces are acting on it but the acceleration due to the forces is in an upward direction.
So we can write,
 $ T - Mg = Ma $
Therefore we can rearrange it as,
 $ T = Ma + Mg $
Taking $ M $ common in the RHS we have,
 $ T = M\left( {a + g} \right) $
Now we can equate the tension in both the cases as the string is the same. So we get,
 $ M\left( {a + g} \right) = 2M\left( {g - a} \right) $
We can cancel the $ M $ from both the LHS and the RHS. So we get,
 $ a + g = 2g - 2a $
Taking the like terms on one side we get,
 $ a + 2a = 2g - g $
Therefore we have,
 $ 3a = g $
Hence the acceleration is
 $ a = \dfrac{g}{3} $
So the mass $ M $ accelerates at the rate of $ \dfrac{g}{3}m/{s^2} $ .

Note
In this problem we have considered the pulley and the string to be massless and there is no friction acting between any of the surfaces. The tension in the string is the same in both cases because the string is considered to be inextensible.