Question

Find the acceleration of $a$, $b$ and $c$ when the string between $A$ and $B$ is cut.

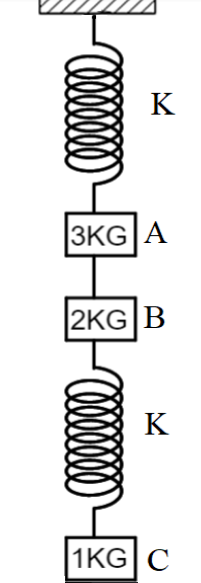
Answer 1

Hint:At first, we'll assume that all forces are in equilibrium, meaning that there is no net force acting on the item and that they are perfectly balanced. Then we must draw the free body diagram and find the acceleration of each block separately. The tension in the string will reach zero when we cut it.

Complete step by step answer:
First we will consider the system is in equilibrium condition.Now we will find the net extension in the spring.Let us first draw the free body diagram of block $C$ .

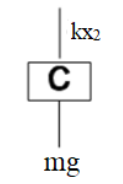
Now we know that one component of $mg$ will act in the downward direction and one component of spring force will act in the upward direction , let it be $k{x_2}$.On balancing the force we will get our equation.Therefore,
$k{x_2} = mg$ …… $\left( 1 \right)$

Now we will combine the blocks $A$ and $B$ together and draw the free body diagram.

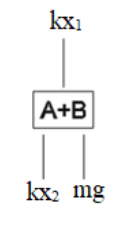
Now here $2mg$ is acting in the downward direction that is one of block $A$ and other of block $B$ , one spring force will act in the downward direction which is $k{x_2}$ because spring is same and other in upward direction, let it be $k{x_1}$.Now on balancing the force we will get our second equation.Therefore,
$2mg + k{x_2} = k{x_1}$ ……. $\left( 2 \right)$

Now we will put the value of $k{x_2}$ from the equation $\left( 1 \right)$ in question $\left( 2 \right)$.
Therefore, $2mg + mg = k{x_1}$.
So we will get the value of $k{x_1} = 3mg$.
Now when we cut the string between $A$ and $B$ , the elongation in spring does not change just after cutting the string.

Now let us draw a free body diagram of block $A$ .

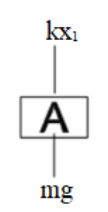
On balancing the components of forces of block $A$ we will get an equation.
That is $mg - k{x_1} = m{a_A}$ ,
Here ${a_A}$ is acceleration of block $A$ .
Put the value of $k{x_1}$ .
Therefore, $mg - 3mg = m{a_A}$
That is $ - 2mg = m{a_A}$
On solving we will get ${a_A} = - 2g$ $m/{s^2}$. Here acceleration is negative therefore it will be in the upward direction.

Now free body diagram for block $B$.

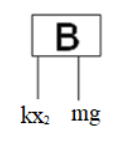
On balancing the components of forces of block $B$ the equation will be
That is $mg + k{x_2} = m{a_B}$
On putting the value of $k{x_2}$ we will get,
That is $mg + mg = m{a_B}$
On solving this we will get ${a_B} = 2g$
So the acceleration of block $B$ is $2g$ $m/{s^2}$ in the downward direction.

Now free body diagram of block $C$.

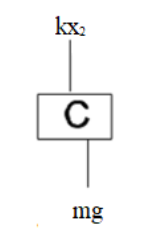
On balancing the force components of block $C$ the equation will be
That is $mg - k{x_2} = m{a_C}$
Or $mg - mg = m{a_C}$ , since $k{x_2} = mg$
On solving we will get ${a_C} = 0$ .
So the acceleration of block $C$ will be zero.

Note:It is necessary to draw a free body diagram as it helps to write the equation of balanced force. Don’t get confused while considering the direction of forces and acceleration, positive value of force and acceleration means the direction is upward and negative value means the direction is downward. Always remember the tension will become zero whenever the string is cut.