
How do you find the absolute value of the complex number $-4+i$ ?
Answer
559.2k+ views
Hint: In this question, we have to find the absolute value of a complex number. As we know, complex numbers are those numbers that contain the real part and the imaginary part. It is expressed in the form of $a+ib$ , where a and b are real numbers and $i$ (iota) is the imaginary unit. The absolute value of a complex number is defined as the distance between the origin (0,0) and the point in the complex number (a,b), it is denoted $|z|=|a+ib|$ . Thus, to solve this problem, we first draw the graph of the coordinates $(0,0\text{) and (}-4,1)$ , and then we will join all the points and form a triangle ABC. After that, we will apply the Pythagoras theorem${{(hypotenuse)}^{2}}={{(base)}^{2}}+{{(perpendicular)}^{2}}$and make the necessary calculations to get the value of hypotenuse, which is the absolute value of the complex number
Complete answer:
According to the question, we have to find the absolute value of the complex number.
The absolute value of a complex number is defined as the distance between the origin (0,0) and the point in the complex number (a,b).
Thus, we will use the Pythagoras theorem ${{(hypotenuse)}^{2}}={{(base)}^{2}}+{{(perpendicular)}^{2}}$, to solve this problem.
The equation of the complex number given to us is $-4+i$ --------- (1)
In addition, the general equation of the complex number is $a+ib$ -------- (2), where a and b are the real numbers and $i$ (iota) is the imaginary unit.
Thus, on comparing equations (1) and (2), we get
$a=-4$ and $b=1$
Therefore, the graph of the equation $-4+i$ with the coordinates $A(-4,1)$ and $B(0,0)$ . We take the y-axis as the imaginary axis and the x-axis as the real axis. We join both the coordinates as shown in the figure.
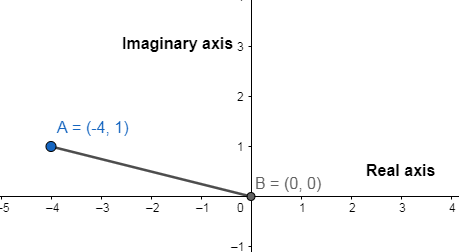
Now, we will form a triangle as shown in the graph and then apply the pythagorean theorem ${{(hypotenuse)}^{2}}={{(base)}^{2}}+{{(perpendicular)}^{2}}$ in the triangle ABC, we will get
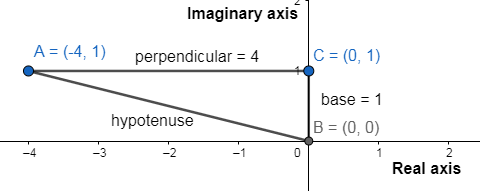
In the triangle ABC, we see that BA=x is the hypotenuse, AC=4 is the perpendicular and CB=1 is the base , therefore we now apply the Pythagoras theorem, we get
$\begin{align}
& \Rightarrow {{(hypotenuse)}^{2}}={{(base)}^{2}}+{{(perpendicular)}^{2}} \\
& \Rightarrow {{(BA)}^{2}}={{(CB)}^{2}}+{{(AC)}^{2}} \\
\end{align}$
Therefore, we substitute the value of the BA, AC, and CB in above equation, we get
$\Rightarrow {{(BA)}^{2}}={{(1)}^{2}}+{{(4)}^{2}}$
On further simplification, we get
$\begin{align}
& \Rightarrow {{(BA)}^{2}}=1+16 \\
& \Rightarrow {{(BA)}^{2}}=17 \\
\end{align}$
Now, taking square root on both sides of the above equation, we get
$\begin{align}
& \Rightarrow \sqrt{{{(BA)}^{2}}}=\sqrt{(17)} \\
& \Rightarrow BA=\sqrt{17} \\
\end{align}$
Therefore, we get
$\Rightarrow BA=4.123$
Therefore, the absolute value of the complex number $-4+i$ is $|z|=|-4+i|=4.123$ , which is our required answer.
Note: In this question, do all the calculations properly to avoid errors. You can also use the distance formula to find the absolute value of the complex number, which is the square root of the sum of the real part squared and the imaginary part squared.
Complete answer:
According to the question, we have to find the absolute value of the complex number.
The absolute value of a complex number is defined as the distance between the origin (0,0) and the point in the complex number (a,b).
Thus, we will use the Pythagoras theorem ${{(hypotenuse)}^{2}}={{(base)}^{2}}+{{(perpendicular)}^{2}}$, to solve this problem.
The equation of the complex number given to us is $-4+i$ --------- (1)
In addition, the general equation of the complex number is $a+ib$ -------- (2), where a and b are the real numbers and $i$ (iota) is the imaginary unit.
Thus, on comparing equations (1) and (2), we get
$a=-4$ and $b=1$
Therefore, the graph of the equation $-4+i$ with the coordinates $A(-4,1)$ and $B(0,0)$ . We take the y-axis as the imaginary axis and the x-axis as the real axis. We join both the coordinates as shown in the figure.
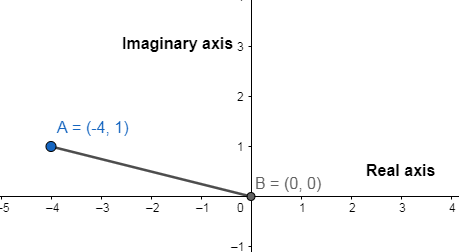
Now, we will form a triangle as shown in the graph and then apply the pythagorean theorem ${{(hypotenuse)}^{2}}={{(base)}^{2}}+{{(perpendicular)}^{2}}$ in the triangle ABC, we will get

In the triangle ABC, we see that BA=x is the hypotenuse, AC=4 is the perpendicular and CB=1 is the base , therefore we now apply the Pythagoras theorem, we get
$\begin{align}
& \Rightarrow {{(hypotenuse)}^{2}}={{(base)}^{2}}+{{(perpendicular)}^{2}} \\
& \Rightarrow {{(BA)}^{2}}={{(CB)}^{2}}+{{(AC)}^{2}} \\
\end{align}$
Therefore, we substitute the value of the BA, AC, and CB in above equation, we get
$\Rightarrow {{(BA)}^{2}}={{(1)}^{2}}+{{(4)}^{2}}$
On further simplification, we get
$\begin{align}
& \Rightarrow {{(BA)}^{2}}=1+16 \\
& \Rightarrow {{(BA)}^{2}}=17 \\
\end{align}$
Now, taking square root on both sides of the above equation, we get
$\begin{align}
& \Rightarrow \sqrt{{{(BA)}^{2}}}=\sqrt{(17)} \\
& \Rightarrow BA=\sqrt{17} \\
\end{align}$
Therefore, we get
$\Rightarrow BA=4.123$
Therefore, the absolute value of the complex number $-4+i$ is $|z|=|-4+i|=4.123$ , which is our required answer.
Note: In this question, do all the calculations properly to avoid errors. You can also use the distance formula to find the absolute value of the complex number, which is the square root of the sum of the real part squared and the imaginary part squared.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




