Question

Find \[\sqrt {3969}\] by the long division method.

Answer 1

Hint: Write the given number into pairs, starting from the right ends. Think of the largest number whose square is equal to just less than the first pair. Subtract the product of divisor and quotient from the first pair. Bring down the next pair to the right of the remainder and so on.

Complete step-by-step solution -
There are the following steps to obtain the value of \[\sqrt {3969}\] using a long division method.
(a) Write the number 3969 as \[\overline {39} \,\,\overline {69}\].
(b). Find the number whose square is just equal or less than 39, which is 6.
(c) Put 6 on the top and also write 6 as a divisor.
(d) The square of 6 is 36. Now subtract 36 from 39.
(e) Now, add 6 with 6 to obtain the next divisor. Then, substitute 69 after the remainder 3.
(f) Now, put 3 at top and after 12 in the next divisor.
(g) Multiply 3 with 123 and subtract from 369.
(h) The remainder becomes 0 and 63 is square root of 3969.
The above procedure is shown below.

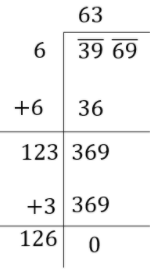
Thus, the value of the expression \[\sqrt {3969}\] is 63.

Note: The first divisor is chosen in such a way that its square is always less or equal to the first pair. We can solve the above problem using L.C.M. method also. Here we can use the prime factorisation method for finding the square root of 3969 in which we find the prime factors but in the question it is asked about using the division method. So, we skip this method.