Question

How do you find slope and intercepts to graph $-3x-5y=6$ ?

Answer 1

Hint: We have been given the equation of a straight-line which is in the standard form. In order to find the slope and intercept of the equation to graph it, we must convert the equation to slope-intercept form. Further, we shall also find the intercepts of the given equation. Hence, we must have proper knowledge of the various forms of equations of straight-line including the standard form and the slope-intercept form.

Complete step by step solution:
The standard form of a line is given as:
$ax+by=c=0$
Where,
$a=$ coefficient of x-variable
$b=$ coefficient of y-variable
$c=$ constant term
We can put various values of x or y-variable to find that particular point on line. If we input the value of both the x and y-component of the point, we can also verify whether that point belongs to that particular line or not.
The slope-intercept form of a line is expressed as:
$y=mx+c$
Where,
$m=$ slope of line
$c=$ intercept of the line
We shall make changes to our given equation, $-3x-5y=6$ accordingly.
Taking the term with x-variable to right hand side of equation, we get
$\Rightarrow -5y=3x+6$
We will now divide the whole equation by -5 to make the coefficient of y equal to 1:
$\Rightarrow y=-\dfrac{3}{5}x-\dfrac{6}{5}$
Therefore, the equation, $-3x-5y=6$ is converted into its slope-intercept form as $y=-\dfrac{3}{5}x-\dfrac{6}{5}$.
We shall put $x=0$ in this equation to calculate the y-intercept of the equation.
$\Rightarrow y=-\dfrac{3}{5}\left( 0 \right)-\dfrac{6}{5}$
$\Rightarrow y=-\dfrac{6}{5}$
Also, we shall put $y=0$ in this equation to calculate the x-intercept of the equation.
$\Rightarrow \left( 0 \right)=-\dfrac{3}{5}x-\dfrac{6}{5}$
$\Rightarrow \dfrac{3}{5}x=-\dfrac{6}{5}$
$\Rightarrow x=-2$
Therefore, the x-intercept is -2 and the y-intercept is $-\dfrac{6}{5}$.
Therefore, using this information, the graph of $-3x-5y=6$ is plotted as:

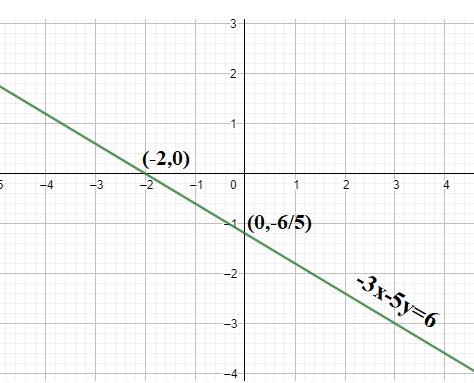
Note:
The equation of a straight line is expressed especially in an intercept form which is given as $\dfrac{x}{a}+\dfrac{y}{b}=1$ where $a$ is the x-intercept of line and $b$ is the y-intercept of the line as mentioned before. One possible mistake we could have done while sketching the graph was plotting the x-intercept as 2 instead of -2.