Question

How do you find sin, cos, tan, sec, cosec, and cot gave (-4, -4)?

Answer 1

Hint: For a given point (x, y), the straight line formed by the origin and the point will make an angle $\theta$ with the horizontal axis. By using the projection of this straight line on both the axes, we can find out the opposite side and adjacent side.
With these data, we can calculate the trigonometric functions for the given point.

Complete Step by Step Solution:
Let us plot the given point (-4, -4) in a Cartesian coordinate system.

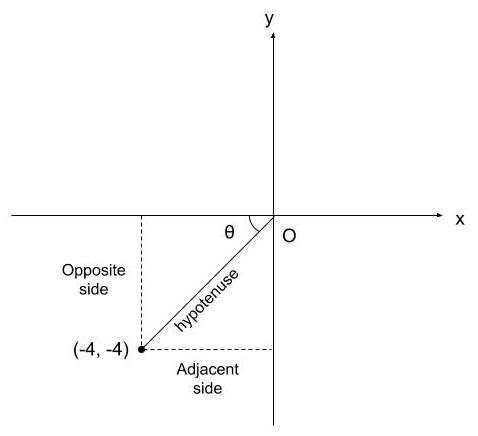
As we can see from the diagram, the straight formed by the origin and the given point makes an angle $\theta$ with the horizontal axis of the coordinate system.
Also, the opposite side and the adjacent side can be seen in the diagram. By using those we can also find out the hypotenuse.
From the figure,
Opposite side, $x=-4$
Adjacent side, $y=-4$ and
The hypotenuse, $h=\sqrt{{{\left( -4 \right)}^{2}}+{{\left( -4 \right)}^{2}}}=4\sqrt{2}$
Now we have all the data required to find the trigonometric ratios for the given point. We know the trigonometric functions
$\Rightarrow \sin \theta =\dfrac{\text{opposite side}}{\text{hypotenuse}}=\dfrac{-4}{4\sqrt{2}}=-\dfrac{1}{\sqrt{2}}$
$\Rightarrow \cos \theta =\dfrac{\text{adjacent side}}{\text{hypotenuse}}=\dfrac{-4}{4\sqrt{2}}=-\dfrac{1}{\sqrt{2}}$
$\Rightarrow \tan \theta =\dfrac{\text{opposite side}}{\text{adjacent side}}=\dfrac{-4}{-4}=1$
$\Rightarrow \text{cosec}\theta =\dfrac{1}{\sin \theta }=\dfrac{1}{-{}^{1}/{}_{\sqrt{2}}}=-\sqrt{2}$
$\Rightarrow \sec \theta =\dfrac{1}{\cos \theta }=\dfrac{1}{-{}^{1}/{}_{\sqrt{2}}}=-\sqrt{2}$
$\Rightarrow \cot \theta =\dfrac{1}{\tan \theta }=\dfrac{1}{1}=1$
By using the above method, we can calculate the trigonometric ratios for any given point in the Cartesian coordinate system. All we have to do is to find out the opposite side and the adjacent side projections of the line formed by the origin and the given point. And we should be familiar with the trigonometric functions.

Note:
From the diagram, we can see that the signs of the adjacent side and the opposite side are changing according to their quadrants. Hence we should not ignore the sign of these sides while calculating the trigonometric ratios.