Question

Find sets A,B and C such that $A\cap B$, $B\cap C$ and $A\cap C$ are non-empty sets and $A\cap B\cap C=\varnothing $.

Answer 1

Hint: Here we assume a universal set $U=\left\{ a,b,c,d,e,f,g \right\}$ and then assume subsets of $U$ as $A,B$ and $C$ such that $A\cap B$, $B\cap C$ and $A\cap C$ are non-empty sets and $A\cap B\cap C=\varnothing $. So, after assuming sets $A,B$ and $C$, we get $A\cap B$, $B\cap C$ and $A\cap C$, and then proceed according to the question.

Complete step-by-step solution:
Now as we assumed a universal set $U=\left\{ a,b,c,d,e,f,g \right\}$, let us now assume –
$\begin{align}
  & A=\left\{ a,b,c,d \right\} \\
 & B=\left\{ b,d,e,g \right\} \\
 & C=\left\{ b,e,f,a \right\} \\
\end{align}$
First, we will find the intersection of sets. The intersection of two sets contains the elements that are common to both the sets.
Now we will get an intersection of $A$ and $B$, $B$ and $C$, and $A$ and $C$.
So, in set A and set B, we have b and d as common, so we get
$A\cap B=\left\{ b,d \right\}$
Now, in set B and set C, we have b and e as common, so we get
$B\cap C=\left\{ b,e \right\}$
And, in set C and set A, we have a and b as common, so we get
$A\cap C=\left\{ a,b \right\}$
As we can see that number of elements in sets $A\cap B$, $B\cap C$ and $A\cap C$are $2$,
$\begin{align}
  & n\left( A\cap B \right)=2 \\
 & n\left( B\cap C \right)=2 \\
 & n\left( A\cap C \right)=2 \\
\end{align}$
So, these are non-empty sets. Now we will get intersection of $A,B$ and $C$. While observing sets A, B and C, we get that element b is the only common element, so we get –
$A\cap B\cap C=\left\{ b \right\}$
So, we have the number of elements in set as
$n\left( A\cap B\cap C \right)=1$
Here, number of elements in $A\cap B\cap C$ is $1$, so it is not a null set. So we have to remove that element which is in $A\cap B\cap C$ from any set.
Let us remove that element which is $b$ from set $C$.
So, $\begin{align}
  & A=\left\{ a,b,c,d \right\} \\
 & B=\left\{ b,d,e,g \right\} \\
 & C=\left\{ e,f,a \right\} \\
\end{align}$
$\begin{align}
  & A\cap B=\left\{ b,d \right\} \\
 & B\cap C=\left\{ e \right\} \\
 & A\cap C=\left\{ a \right\} \\
\end{align}$ and $\begin{align}
  & n\left( A\cap B \right)=2\ne 0 \\
 & n\left( B\cap C \right)=2\ne 0 \\
 & n\left( A\cap C \right)=2\ne 0 \\
\end{align}$
So, $\begin{align}
  & A\cap B\cap C=\varnothing \\
 & n\left( A\cap B\cap C \right)=0 \\
\end{align}$
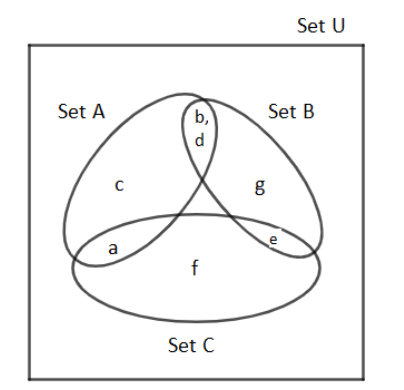
So here, $\begin{align}
  & A=\left\{ a,b,c,d \right\} \\
 & B=\left\{ b,d,e,g \right\} \\
 & C=\left\{ e,f,a \right\} \\
\end{align}$ for which $A\cap B$, $B\cap C$ and $A\cap C$are non-empty set and $A\cap B\cap C=\varnothing $
Therefore, Venn diagram for these sets:

Note: In this type of equation, we should have to take care of the number of elements in each set and take intersection very carefully, because many times we can get confused about sets of which we are getting intersection. So, keep this in mind.
(ii) In this solution, we have taken alphabets as elements, but students are free to take anything as the elements of the sets.