Question

Find scale factor in following image.

Answer 1

Hint: Find out if the shapes given are similar or not. If not similar the scale factor cannot be found out. If the given shapes are similar scale factor is the ratio of any corresponding side of the two figures.
In coordinate geometry, we have shapes, both two – dimensional and three – dimensional. Scale factor in geometry is used for comparative figures which have the same shapes but varying lengths.

Complete step by step solution:
The scale factor is defined as the number which is multiplied by the original number to produce a smaller or greater value than the original number.
The scale factor is defined as the number which is multiplied by the original number to produce a smaller or greater value than the original number.
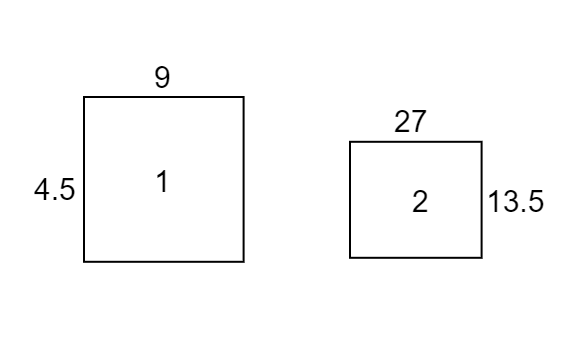
Let us assume the two rectangles given above as ${{r}_{1}},{{r}_{2}}$ . We can see that the two figures are similar. Hence, a scale factor can be found out.
The Scale factor of the two rectangles ${{r}_{1}},{{r}_{2}}$ is calculated by dividing the corresponding lengths of rectangle ${{r}_{2}}$ with rectangle ${{r}_{1}}$.
The formula for the scale factor is given by,
Scale factor = $\dfrac{\left(\text{side length of rectangle }{r}_{2}\right)}{\left(\text{side length of rectangle } {r}_{1}\right)}$ in correspondence.
We say sides (${{s}_{1}},{{s}_{2}}$) of two rectangles ${{r}_{1}},{{r}_{2}}$ are corresponding sides if they share the same relative position in the two figures.
In the above image, we see that $\left( 9,27 \right);\left( 4.5,13.5 \right)$ share the same relative position. Hence, they are corresponding sides.
$\Rightarrow$ Scale factor = $\dfrac{27}{9}=3$
Alternatively,
$\Rightarrow$ Scale factor = $\dfrac{13.5}{4.5}=3$
Hence, the scale factor for the given figures is 3.

Note: Finding out the corresponding sides of the two figures is necessary to calculate the scale factor. The scale factor can only be found out if the two figures are similar. One must keep in mind that the scale factor obtained should be the same for all the corresponding sides.