
Find rest of the values of x when one root of \[{{x}^{4}}-4{{x}^{2}}+8x+35=0\] is given which is \[2+i\sqrt{3}\]
Answer
598.8k+ views
Hint: To find the roots of a polynomial when one complex root is given we need to use the conjugate pair theory or more precisely we should use the given root to form a quadratic equation which have conjugate roots and one of them is the given root which is \[2+i\sqrt{3}\] and hence the conjugate will be \[2-i\sqrt{3}\] ,and now further use the long division method to find the rest of the roots of the polynomial.
Complete step-by-step answer:
Long division method is simple division but with the use of polynomials, the method is the same, put one term in quotient place and multiply each divisor term one at a time with it.
Now the given polynomial equation is,
\[{{x}^{4}}-4{{x}^{2}}+8x+35=0\]
and the given root is \[2+i\sqrt{3}\]
Now we have \[x=2+i\sqrt{3}\] as a root of the given equation,
Keeping the complex part of the given root on one side of the root equation, we get,
\[x-2=i\sqrt{3}\]
Now squaring both sides of this root equation, we get,
\[\begin{align}
& {{(x-2)}^{2}}={{i}^{2}}3 \\
& {{x}^{2}}+4-4x=-3 \\
& {{x}^{2}}-4x+7=0 \\
\end{align}\] (As\[i=\sqrt{-1}\], so \[{{i}^{2}}=-1\])
This quadratic equation has complex roots which are conjugate to each other. By solving the equation using a quadratic formula we find that the roots are\[2\pm i\sqrt{3}\].
Now this quadratic equation is one of the roots of the given polynomial, hence we can divide the given polynomial with this quadratic equation and get to know the other roots of this given polynomial.
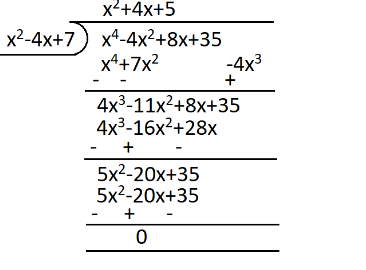
In division there is always change in sign of every number you get when you multiply divisor and quotient.
Now the other root of the given polynomial is another quadratic equation which is,
\[({{x}^{2}}+4x+5)\]
Now by using the Euclid's division lemma, we get,
Euclid’s division lemma is, we can represent the \[\dfrac{a}{b}\] ratio as \[a=bq+r\] where q is quotient and r is remainder.
So, the equation we will get is,
\[{{x}^{4}}-4{{x}^{2}}+8x+35=({{x}^{2}}+4x+5)({{x}^{2}}-4x+7)\]
The roots of the quadratic equations divide the given polynomial as they are it's factors represented in the above equation.
Now to find the actual complex roots of the given polynomial we need to solve these two quadratic equations and their roots will satisfy the given polynomial which we can even check by dividing the polynomial by taking one or product of more than one at a time.
The roots of the quadratic equation, \[{{x}^{2}}-4x+7=0\] are,
By using quadratic formula, we get,
Quadratic formula, \[x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}\] on the equation \[a{{x}^{2}}+bx+c=0\]
Hence by using the formula in the equation \[{{x}^{2}}-4x+7=0\], we get,
\[\begin{align}
& x=\dfrac{-(-4)\pm \sqrt{{{(-4)}^{2}}-4(1)(7)}}{2(1)} \\
& x=\dfrac{4\pm \sqrt{16-28}}{2} \\
& x=\dfrac{4\pm \sqrt{-12}}{2} \\
& x=\dfrac{4\pm \sqrt{(4)(3)}\sqrt{-1}}{2} \\
& x=\dfrac{4\pm 2i\sqrt{3}}{2}=2\pm i\sqrt{3} \\
\end{align}\](As \[i=\sqrt{-1}\])
Hence, \[x=2\pm i\sqrt{3}\]
The roots of the other quadratic equation \[{{x}^{2}}+4x+5=0\], are,
By using the quadratic formula, we get,
Quadratic formula, \[x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}\] on the equation \[a{{x}^{2}}+bx+c=0\]
Hence by using the formula in the equation \[{{x}^{2}}+4x+5=0\], we get,
\[\begin{align}
& x=\dfrac{-(4)\pm \sqrt{{{(4)}^{2}}-4(1)(5)}}{2(1)} \\
& x=\dfrac{-4\pm \sqrt{16-20}}{2} \\
& x=\dfrac{-4\pm \sqrt{-4}}{2} \\
& x=\dfrac{-4\pm \sqrt{4}\sqrt{-1}}{2} \\
& x=\dfrac{-4\pm 2i}{2}=-2\pm i \\
\end{align}\] (As \[i=\sqrt{-1}\])
Hence, \[x=-2\pm i\]
Therefore, the four roots of the given polynomial are,
\[\begin{align}
& x=2+i\sqrt{3} \\
& x=2-i\sqrt{3} \\
& x=-2-i \\
& x=-2+i \\
\end{align}\]
Note: Now, we did not divide the given polynomial with the given root because it would have been very difficult and also we would have ended up with a cubic equation whose roots are more difficult to find as compared to the quadratic equation.Look out to change signs of coefficients you get from multiplying quotients by divisor. Every sign should be reversed once.
We can always use completing the square method or Quadratic formula to find complex roots of quadratic equations. Do not go for factorization as some equations take time to get solved with this method. Below is the glimpse of Completing the square method and the steps involve –
Making the coefficient of \[{{x}^{2}}\] 1 and positive then add and subtract square of half times the coefficient of x, you will observe the formula identity of \[{{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab\] getting completed, shift the rest of the terms to R.H.S. of equation then at last find the value of x by taking square root on both sides. To save time, always go for the Quadratic formula.
\[\begin{align}
& a{{x}^{2}}+bx+c=0 \\
& {{x}^{2}}+\dfrac{b}{a}x+\dfrac{c}{a}=0 \\
& {{x}^{2}}+{{\left( \dfrac{b}{2a} \right)}^{2}}+\dfrac{b}{a}x+\dfrac{c}{a}-{{\left( \dfrac{b}{2a} \right)}^{2}}=0 \\
& {{x}^{2}}+{{\left( \dfrac{b}{2a} \right)}^{2}}+\left( 2 \right)\dfrac{b}{2a}x+\dfrac{c}{a}-{{\left( \dfrac{b}{2a} \right)}^{2}}=0 \\
& \left[ {{\left( x+\dfrac{b}{2a} \right)}^{2}} \right]={{\left( \dfrac{b}{2a} \right)}^{2}}-\dfrac{c}{a} \\
\end{align}\]
You can also check your answer if it is correct or not by putting the values of the roots calculated.
Complete step-by-step answer:
Long division method is simple division but with the use of polynomials, the method is the same, put one term in quotient place and multiply each divisor term one at a time with it.
Now the given polynomial equation is,
\[{{x}^{4}}-4{{x}^{2}}+8x+35=0\]
and the given root is \[2+i\sqrt{3}\]
Now we have \[x=2+i\sqrt{3}\] as a root of the given equation,
Keeping the complex part of the given root on one side of the root equation, we get,
\[x-2=i\sqrt{3}\]
Now squaring both sides of this root equation, we get,
\[\begin{align}
& {{(x-2)}^{2}}={{i}^{2}}3 \\
& {{x}^{2}}+4-4x=-3 \\
& {{x}^{2}}-4x+7=0 \\
\end{align}\] (As\[i=\sqrt{-1}\], so \[{{i}^{2}}=-1\])
This quadratic equation has complex roots which are conjugate to each other. By solving the equation using a quadratic formula we find that the roots are\[2\pm i\sqrt{3}\].
Now this quadratic equation is one of the roots of the given polynomial, hence we can divide the given polynomial with this quadratic equation and get to know the other roots of this given polynomial.
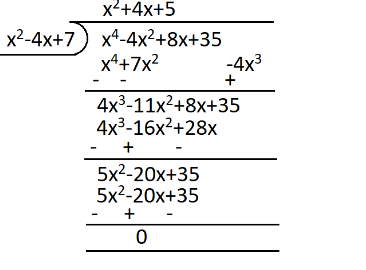
In division there is always change in sign of every number you get when you multiply divisor and quotient.
Now the other root of the given polynomial is another quadratic equation which is,
\[({{x}^{2}}+4x+5)\]
Now by using the Euclid's division lemma, we get,
Euclid’s division lemma is, we can represent the \[\dfrac{a}{b}\] ratio as \[a=bq+r\] where q is quotient and r is remainder.
So, the equation we will get is,
\[{{x}^{4}}-4{{x}^{2}}+8x+35=({{x}^{2}}+4x+5)({{x}^{2}}-4x+7)\]
The roots of the quadratic equations divide the given polynomial as they are it's factors represented in the above equation.
Now to find the actual complex roots of the given polynomial we need to solve these two quadratic equations and their roots will satisfy the given polynomial which we can even check by dividing the polynomial by taking one or product of more than one at a time.
The roots of the quadratic equation, \[{{x}^{2}}-4x+7=0\] are,
By using quadratic formula, we get,
Quadratic formula, \[x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}\] on the equation \[a{{x}^{2}}+bx+c=0\]
Hence by using the formula in the equation \[{{x}^{2}}-4x+7=0\], we get,
\[\begin{align}
& x=\dfrac{-(-4)\pm \sqrt{{{(-4)}^{2}}-4(1)(7)}}{2(1)} \\
& x=\dfrac{4\pm \sqrt{16-28}}{2} \\
& x=\dfrac{4\pm \sqrt{-12}}{2} \\
& x=\dfrac{4\pm \sqrt{(4)(3)}\sqrt{-1}}{2} \\
& x=\dfrac{4\pm 2i\sqrt{3}}{2}=2\pm i\sqrt{3} \\
\end{align}\](As \[i=\sqrt{-1}\])
Hence, \[x=2\pm i\sqrt{3}\]
The roots of the other quadratic equation \[{{x}^{2}}+4x+5=0\], are,
By using the quadratic formula, we get,
Quadratic formula, \[x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}\] on the equation \[a{{x}^{2}}+bx+c=0\]
Hence by using the formula in the equation \[{{x}^{2}}+4x+5=0\], we get,
\[\begin{align}
& x=\dfrac{-(4)\pm \sqrt{{{(4)}^{2}}-4(1)(5)}}{2(1)} \\
& x=\dfrac{-4\pm \sqrt{16-20}}{2} \\
& x=\dfrac{-4\pm \sqrt{-4}}{2} \\
& x=\dfrac{-4\pm \sqrt{4}\sqrt{-1}}{2} \\
& x=\dfrac{-4\pm 2i}{2}=-2\pm i \\
\end{align}\] (As \[i=\sqrt{-1}\])
Hence, \[x=-2\pm i\]
Therefore, the four roots of the given polynomial are,
\[\begin{align}
& x=2+i\sqrt{3} \\
& x=2-i\sqrt{3} \\
& x=-2-i \\
& x=-2+i \\
\end{align}\]
Note: Now, we did not divide the given polynomial with the given root because it would have been very difficult and also we would have ended up with a cubic equation whose roots are more difficult to find as compared to the quadratic equation.Look out to change signs of coefficients you get from multiplying quotients by divisor. Every sign should be reversed once.
We can always use completing the square method or Quadratic formula to find complex roots of quadratic equations. Do not go for factorization as some equations take time to get solved with this method. Below is the glimpse of Completing the square method and the steps involve –
Making the coefficient of \[{{x}^{2}}\] 1 and positive then add and subtract square of half times the coefficient of x, you will observe the formula identity of \[{{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab\] getting completed, shift the rest of the terms to R.H.S. of equation then at last find the value of x by taking square root on both sides. To save time, always go for the Quadratic formula.
\[\begin{align}
& a{{x}^{2}}+bx+c=0 \\
& {{x}^{2}}+\dfrac{b}{a}x+\dfrac{c}{a}=0 \\
& {{x}^{2}}+{{\left( \dfrac{b}{2a} \right)}^{2}}+\dfrac{b}{a}x+\dfrac{c}{a}-{{\left( \dfrac{b}{2a} \right)}^{2}}=0 \\
& {{x}^{2}}+{{\left( \dfrac{b}{2a} \right)}^{2}}+\left( 2 \right)\dfrac{b}{2a}x+\dfrac{c}{a}-{{\left( \dfrac{b}{2a} \right)}^{2}}=0 \\
& \left[ {{\left( x+\dfrac{b}{2a} \right)}^{2}} \right]={{\left( \dfrac{b}{2a} \right)}^{2}}-\dfrac{c}{a} \\
\end{align}\]
You can also check your answer if it is correct or not by putting the values of the roots calculated.
Recently Updated Pages
Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE

What is the full form of pH?




