Question

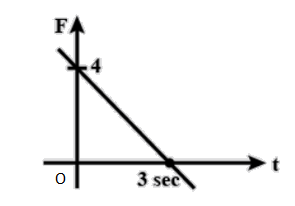
Find relation between force (\[F\] ) and time (\[t\] ) as shown in figure.

A. $\dfrac{F}{3} + \dfrac{t}{4} = 1$
B. $3F + 4t = 12$
C. $F + 4t - 1 = 0$
D. None

Answer 1

Hint:To find the relation between F and t, we can change the equation $F = mt + c$in \[F\] and \[t\] with the help of differentiation. After that we can find the values of all the variables in the new equation (in \[F\]and \[t\]) by reading the given graph.

Complete step-by-step solution:
Let the mass of the body is\[m\] . Let $F$ is the force on the body. The body experiences the force of \[4\] unit after \[3\] unit time.
We know that the relation between force and time is given as-
$F = mt + c$ (i)
Let us differentiate the equation. We can get the following equation.
$\Delta F = m\Delta t$
Or we can write the above equation as
$m = \dfrac{{\Delta F}}{{\Delta t}}$
Substituting the value of \[m\] in equation (i), we get-
$F = \dfrac{{\Delta F}}{{\Delta t}}t + c$ (ii)
For solving the above equation, we have to find the value of $\Delta F$ and $\Delta t$ . So, for calculating the values of $\Delta F$ and $\Delta t$, we can observe the given graph.
When $t = 0$,
$F = 4$
And when $t = 3$,
$F = 0$
So, Using the above values, we can find -
$\Delta F = F(t) - F(0)$
$ \Rightarrow \Delta F = 0 - 4$
And $\Delta t = 3 - 0$
So, putting the values of $\Delta F$ and $\Delta t$ in the equation (ii), we get-
$F = \dfrac{{ - 4t}}{3} + c$ (iii)
But from the graph-
At $t = 0$and $F = 4$. So, putting these values in equation (i), we get-
$4 = m \times 0 + c$
Or $c = 4$
So, putting the value of \[c\] in the equation (iii), we get-
$F = \dfrac{{ - 4t}}{3} + 4$
Simplifying the above equation, we get
$3F + 4t = 12$
Hence, option B is correct.

Note:- In this question, we have to change \[m\] in terms of \[F\]and\[t\]. This change gives the whole equation in \[F\] and\[t\] . After changing the equation in \[F\] and\[t\] , we have to read the graph for solving the equation. We have to read the graph minutely as when \[t = 0\] then \[F = 4\] and when \[t = 3\] then\[F = 0\].