Question

Find out the Bulk stress on the spherical object of radius $\dfrac{{10}}{\pi }cm$ if area and mass of piston is $50c{m^2}$ and $52kg$ respectively for a cylinder filled with gas.

(A) $1 \times {10^5}N/{m^2}$
(B) $2 \times {10^5}N/{m^2}$
(C) $3 \times {10^5}N/{m^2}$
(D) $4 \times {10^5}N/{m^2}$

Answer 1

Hint
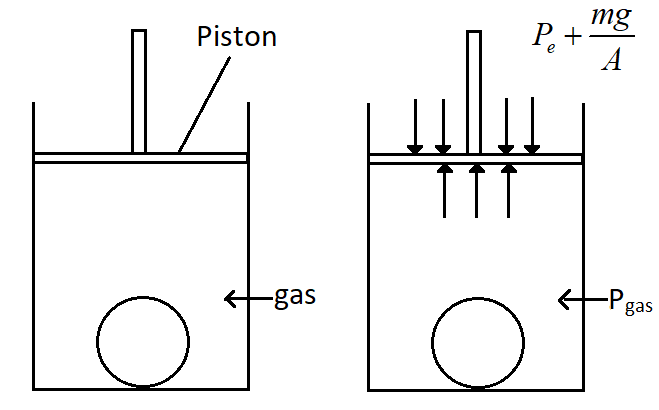
The bulk stress will be the pressure exerted by the gas on the spherical object. So this pressure will be equal to the pressure that is due to the mass of the piston and the pressure due to the atmosphere above the piston.

Formula Used: In this solution we will be using the following formula,
$P = \dfrac{F}{A}$
where $P$ is the pressure,
$F$ is the force and $A$ is the area.

Complete step by step answer
The pressure on any object is the force exerted on the object per unit area of it. Now in the question we are asked to find the bulk stress on the ball. This will be equal to the pressure exerted by the gas in the cylinder that is present above the ball.
This pressure exerted by the gas on the ball will be given by the pressure that is exerted by the weight of the piston and as well as the atmospheric pressure above the piston.
Now, in the question we are given the mass of the piston as $50kg$and the area of the piston is given as, $50c{m^2}$.We can write the area in SI unit as, $A = 50 \times {10^{ - 4}}{m^2}$. So the pressure that is exerted by the piston will be the weight of the piston per unit area. Hence let us consider the pressure due to the piston to be ${P_{piston}}$. So the value of ${P_{piston}}$ will be,
${P_{piston}} = \dfrac{{mg}}{A}$. Let us consider the acceleration due to gravity as, $g = 10m/{s^2}$. So substituting we get,
${P_{piston}} = \dfrac{{50 \times 10}}{{50 \times {{10}^{ - 4}}}}$
On calculating we get,
${P_{piston}} = 1 \times {10^5}N/{m^2}$.
The pressure on the gas is the sum of the pressure due to the piston and the atmospheric pressure. The atmospheric pressure can be considered as, ${P_{atm}} = 1 \times {10^5}Pa$.
So we get the pressure on the gas as,
${P_{gas}} = {P_{piston}} + {P_{atm}}$
Substituting the values we get,
${P_{gas}} = \left[ {\left( {1 \times {{10}^5}} \right) + \left( {1 \times {{10}^5}} \right)} \right]N/{m^2}$
So we get,
${P_{gas}} = 2 \times {10^5}N/{m^2}$
This is the bulk stress on the spherical object.
So the correct answer is option B.

Note
The bulk stress is also called the volume stress. It is the force that acts on a body from all the direction and results in the change in the shape of the body, or deforms the body. This deforming force on the body is termed as volume stress.