Question

Find out the area (in square units) of the region bounded by the parabola, $\,y={{x}^{2}}+2$ and the lines \[y=x+1,\,x=0,\,x=3\]:
A. $\dfrac{15}{4}$
B. $\dfrac{15}{2}$
C. $\dfrac{21}{2}$
D. $\dfrac{17}{4}$

Answer 1

Hint: In order to find the area between the curves we have to do integration between the limits given in the question. For this question we will start by identifying the limits as [0,3] and then integrate the curves (parabola and line) by the basic power rule. After that we will put the upper limit and lower limit to find the area.

Complete step-by-step answer:
Let us draw the graph of the parabola and the lines given in the question, It will look like the following:

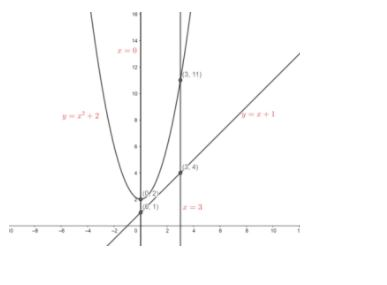
Now we have to find the area bound between these graphs and as we can see the lines x=0 and x=3, these lines shows the limit between which we have to find the area.
So we have to find the area between the curves $\,y={{x}^{2}}+2$ and $y=x+1$ on the interval [0,3]:
Now by the definition of area between the curves we know that:
The area between curves is the area between a curve $f\left( x \right)$ and $g\left( x \right)$ on an interval $\left[ a,b \right]$ is given by
$A=\int_{a}^{b}{|}f\left( x \right)-g\left( x \right)|dx$
Therefore, we will apply this definition to our question:
We have $f\left( x \right)={{x}^{2}}+2$ and $g\left( x \right)=x+1$ and we have the interval obtained as $\left[ 0,3 \right]$:
Therefore, Area between the curves become: $\int\limits_{0}^{3}{\left| \left( {{x}^{2}}+2 \right)-\left( x+1 \right) \right|}dx$
We will solve this integral to obtain our integral for this we will apply the basic property of ontegral that is:
$\int{\left( f\left( x \right)-g\left( x \right) \right)dx=}\int{f\left( x \right)dx-\int{g\left( x \right)dx}}$
Therefore,
 \[\int\limits_{0}^{3}{\left| \left( {{x}^{2}}+2 \right)-\left( x+1 \right) \right|}dx=\int\limits_{0}^{3}{\left| \left( {{x}^{2}}+2 \right) \right|}dx-\int\limits_{0}^{3}{\left| \left( x+1 \right) \right|}dx\]
We will apply the power rule for integration to solve the given integration:
$\int{{{x}^{n}}dx=\dfrac{{{x}^{n+1}}}{n+1}+C}$
On applying this we will get the following:
\[\int\limits_{0}^{3}{\left| \left( {{x}^{2}}+2 \right) \right|}dx-\int\limits_{0}^{3}{\left| \left( x+1 \right) \right|}dx={{\left| \left| \dfrac{{{x}^{3}}}{3}+2x \right|-\left| \dfrac{{{x}^{2}}}{2}+x \right| \right|}^{3}}_{0}\]

We will now put the upper limit and lower limit in the above equation we will have:
\[\begin{align}
  & {{\left| \left| \dfrac{{{x}^{3}}}{3}+2x \right|-\left| \dfrac{{{x}^{2}}}{2}+x \right| \right|}^{3}}_{0} \\
 & \Rightarrow \left| \left( \dfrac{{{3}^{3}}}{3}+2\left( 3 \right) \right)-\left( \dfrac{{{0}^{3}}}{3}+2\left( 0 \right) \right) \right|-\left| \left( \dfrac{{{3}^{2}}}{2}+3 \right)-\left( \dfrac{{{0}^{2}}}{2}+0 \right) \right| \\
 & \Rightarrow 15-\left( \dfrac{15}{2} \right) \\
 & \Rightarrow \dfrac{15}{2} \\
\end{align}\]
Therefore, The area is $\dfrac{15}{2}$ .

So, the correct answer is “Option b”.

Note: Students can get confused while applying the upper limit and the lower limit, first apply the upper limit into the equation and then followed by a negative sign apply the lower limit. Since here our lower limit is 0, calculation is easy but it can get tedious if the limit is something other than 0.