Question

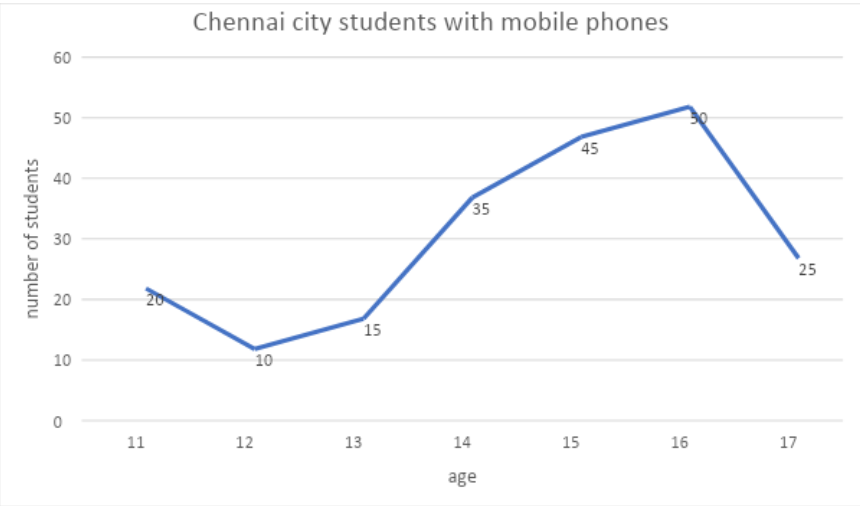
Find out how many students of $14\dfrac{1}{2}$ year olds have mobile phones.

A. 20
B. 30
C. 40
D. 50

Answer 1

Hint: We first find the axes and also find out the variables they represent. Then we find the individual value of the number of students of $14\dfrac{1}{2}$ years between 14 and 15. We find the base of the perpendicular drawn from the top of that point.

Complete step-by-step solution:
In the given graphical representation, there are two axes. The X-axis represents the age of students. There are 7 entries, 11 to 17. The Y-axis represents the number of students.
We need to find out the number of students of $14\dfrac{1}{2}$ year old who have mobile phones.
We first find out the position of the point $14\dfrac{1}{2}$ on the X-axis.
From the marking of the individual bar graphs, we can see that the 14 and 15 have their individual points and the point $14\dfrac{1}{2}$ has a point in between them.
So, the point is exactly in the middle of 14 and 15.
We draw a perpendicular line to the X-axis from the point $14\dfrac{1}{2}$ on the Y-axis.

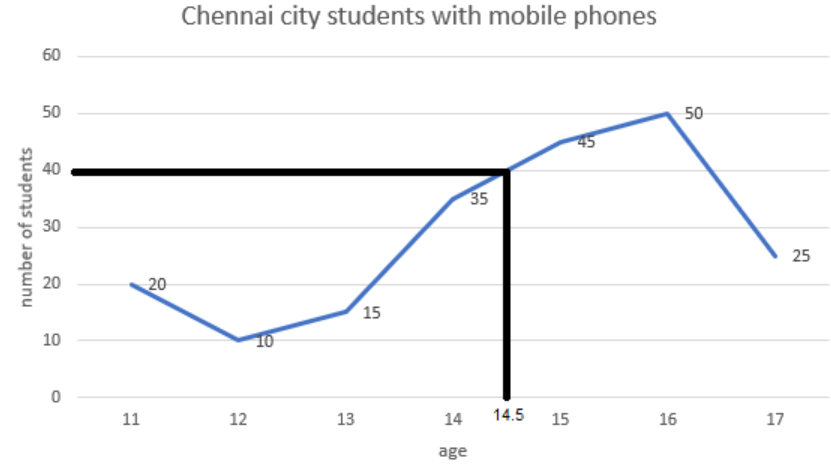
The intersecting point being at the point of 40.
So, 40 students of $14\dfrac{1}{2}$ year olds have mobile phones. The correct option is (C).

Note: If the individual values of those ages are not mentioned then we need to draw a perpendicular line from the top of the points of those individual numbers on the Y-axis to find out the values. The line will touch the axis at a fixed point and that will help to find the exact value. We have a linear line form of the Y-axis from point 35 to 45. The value of the X-axis changes from 14 to 15. So, a unitary change of x gives us a 10-unit change of y in that interval. Being in linear form when we change the value of x from 14 to 14.5, for $\dfrac{1}{2}$ unit change value of y changes 5 units. That’s why the intersecting point is on the point of $35+5=40$.