Question

How do you find missing sides and angles of a non-right triangle, triangle ABC, angle C is 115, side b is 5, side c is 10?

Answer 1

Hint: In this question, we have to find the rest of the missing sides and angles. We will use the sine rule to find all the missing terms as we are given two sides and one angle in this question.
Law of sine:
 $ \Rightarrow \dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C} $

Complete step by step answer:
Let’s solve the question.
First, understand how the law of sine works on triangles.
For any triangle:
In this figure, a, b, c are sides, and A, B and C are the angles.

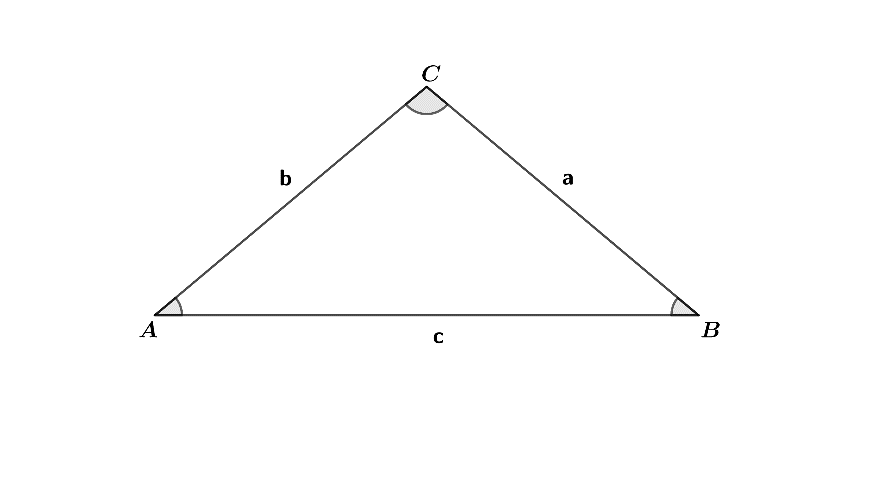
So, it says that when we divide side ‘a’ by the sine of $ \angle A $ it is equal to side ‘b’ divided by the sine of $ \angle B $ and also equal to side ‘c’ divided by the sine of $ \angle C $ .
 $ \Rightarrow \dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C} $
Now, make a figure to see what all terms are given.

According to the law of sine:

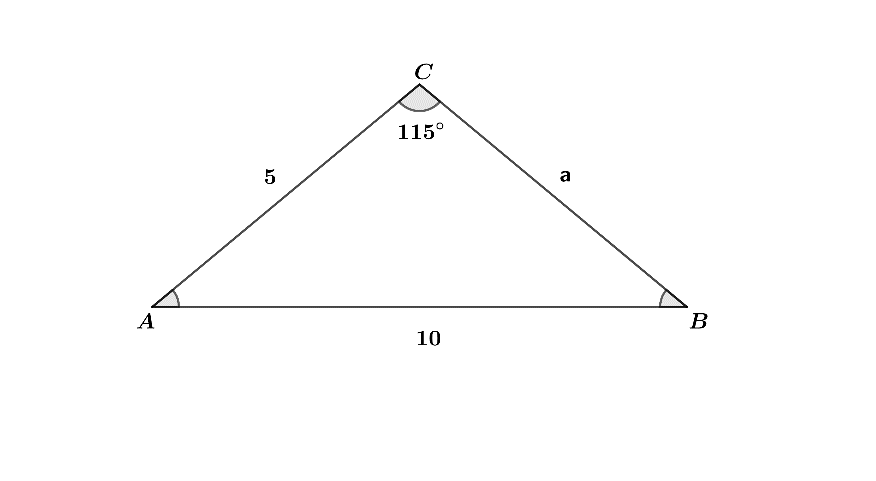
 $ \Rightarrow \dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C} $
As, b = 5, c = 10 and $ \angle C $ = $ {{115}^{\circ }} $ .
 So we have to equate $ \dfrac{b}{\sin B} $ and $ \dfrac{c}{\sin C} $ to find $ \angle B $ .
 $ \Rightarrow \dfrac{b}{\sin B}=\dfrac{c}{\sin C} $
Now put the values:
 $ \Rightarrow \dfrac{5}{\sin B}=\dfrac{10}{\sin {{115}^{\circ }}} $
Now, leave sin B alone.
 $ \Rightarrow 5\times \dfrac{\sin {{115}^{\circ }}}{10}=\sin B $
 $ \Rightarrow \dfrac{0.9063}{2}=\sin B $
 $ \Rightarrow 0.45=\sin B $
Now, use the inverse function of sine.
 $ \Rightarrow {{\sin }^{-1}}0.45=B $
So, B = 26.95
Now, by angle sum property of a triangle, the sum of three angles of a triangle is $ {{180}^{\circ }} $ . So, let’s apply angle sum property to find $ \angle A $ .
 $ \Rightarrow \angle A+\angle B+\angle C={{180}^{\circ }} $
Put the value of B = 26.95 and $ \angle C={{115}^{\circ }} $ :
 $ \Rightarrow \angle A+26.95+{{115}^{\circ }}={{180}^{\circ }} $
 $ \Rightarrow \angle A+141.95={{180}^{\circ }} $
 $ \Rightarrow \angle A={{180}^{\circ }}-141.95 $
 $ \therefore \angle A=38.05 $
Now, we have to find side ‘a’.
As we know:
 $ \Rightarrow \dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C} $
Now, let’s equate $ \dfrac{a}{\sin A} $ and $ \dfrac{c}{\sin C} $
Now, put the value c = 10, $ A=38.05 $ , C = $ {{115}^{\circ }} $ :
 $ \Rightarrow \dfrac{a}{\sin A}=\dfrac{c}{\sin C} $
 $ \Rightarrow \dfrac{a}{\sin 38.05}=\dfrac{10}{\sin {{115}^{\circ }}} $
 $ \begin{align}
  & \Rightarrow \dfrac{a}{0.6163}=\dfrac{10}{0.9063} \\
 & \Rightarrow a=\dfrac{10}{0.9063}\times 0.6163 \\
\end{align} $
After simplifying we get:
 $ \therefore $ a = 6.8
So, our final answer is: a = 6.8, $ \angle B $ = 26.95, $ \angle A=38.05 $ .

Note:
 Students should know the law of sine for this question. A mistake can be made while applying inverse sine function here $ {{\sin }^{-1}}0.45=B $ . Don’t take sine function as it is. We have to apply the inverse function of sine when it goes to the other side of the equation. Be aware of calculation mistakes.