Question

How do you find linear approximation of function ? \[\]

Answer 1

Hint: We recall the Taylor series approximation where approximate an $n$ times differentiable function $f\left( x \right)$ at the point $x=a$with an ${{n}^{th}}$ degree polynomial as $f\left( x \right)=f\left( a \right)+{{f}^{'}}\left( a \right)\left( x-a \right)+{{f}^{''}}\left( a \right)\dfrac{{{\left( x-a \right)}^{2}}}{2!}+...+{{f}^{n}}\left( a \right)\dfrac{{{\left( x-a \right)}^{n}}}{2!}$. We take degree of polynomial 1 to approximate linearly. [\]

Complete step-by-step answer:
We know that if $f\left( x \right)$ is function that is $n$ times differentiable which means the derivative of $f\left( x \right)$ that is $\dfrac{{{d}^{n}}x}{{{\left( dx \right)}^{n}}}f\left( x \right)$exist for $n=1,2,3...$ , then we can approximate the function $f\left( x \right)$ with an $n$ degree polynomial described as ;
\[f\left( x \right)=f\left( a \right)+{{f}^{'}}\left( a \right)\left( x-a \right)+{{f}^{''}}\left( a \right)\dfrac{{{\left( x-a \right)}^{2}}}{2!}+...+{{f}^{n}}\left( a \right)\dfrac{{{\left( x-a \right)}^{n}}}{2!}\]
We know that a linear function has the degree 1. We see that in the above series from the degree of terms from the third term onward is greater than 1. So we can approximate with first two terms as linear polynomial as
\[f\left( x \right)=f\left( a \right)+{{f}^{'}}\left( x \right)\left( x-a \right)\]
Alternative method: We can alternatively approximate the slope-point equation of tangent line at $x=a$. . We know that if a line with slope $m$ passes through a point $\left( {{x}_{1}},{{y}_{1}} \right)$ then its equation is given by
\[y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)\]
 Let us approximate the function $f\left( x \right)$ at $x=a$. We have the function value at $x=a$ that is $f\left( a \right)$.So $\left( a,f\left( a \right) \right)$ becomes a point on the curve. We know that the slope of the tangent line at any point on the curve is given by the derivative value of the curve at that point. So the slope is
\[m={{\left. \dfrac{d}{dx}f\left( x \right) \right|}_{x=a}}={{\left. {{f}^{'}}\left( x \right) \right|}_{x=a}}={{f}^{'}}\left( a \right)\]
We use slope-point equation with $y=f\left( x \right),x=x,{{x}_{1}}=a,{{y}_{1}}=f\left( a \right),m={{f}^{'}}\left( a \right)$and find the equation of tangent line as
\[\begin{align}
  & f\left( x \right)-f\left( a \right)={{f}^{'}}\left( a \right)\left( x-a \right) \\
 & \Rightarrow f\left( x \right)=f\left( a \right)+{{f}^{'}}\left( a \right)\left( x-a \right) \\
\end{align}\]

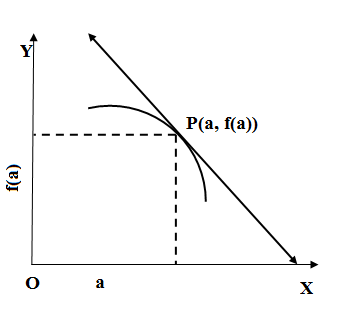
Note: We note that if we approximate the function with a linear polynomial we are assuming the curve as linear and linear approximation is also known as tangent line approximation. If $L\left( x \right)=f\left( a \right)+{{f}^{'}}\left( a \right)\left( x-a \right)$ is the approximation the we get the absolute error as $E=\left| f\left( x \right)-L\left( x \right) \right|$. If $f\left( x \right)$ is concave upward between $x,a$ then $L\left( x \right)$ is an underestimate and if $f\left( x \right)$ is concave upward between $x,a$ like in the diagram above $L\left( x \right)$ is an overestimate.