Question

How do you find legs in a 45-45-90 triangle when its hypotenuse is 11?

Answer 1

Hint: As per the given data, two angles of the triangle are equal and the third angle is ${90^ \circ }$. Thus this is an isosceles right angled triangle with the length of its hypotenuse is given as 11 units. Assume the other two sides of a variable and then use Pythagoras theorem to find its value.

Complete step-by-step solution:
According to the question, specifications of a triangle are given to us. We have to obtain the length of its base.
The angles of the triangle are given as ${45^ \circ }$, ${45^ \circ }$ and ${90^ \circ }$. Since two of its angles are the same and the third one is a right angle, the triangle is a right angled triangle.
The length of its hypotenuse is also given and it is 11 units. Let the lengths of its base and height are both $x$ units. These conditions are shown in the below figure:

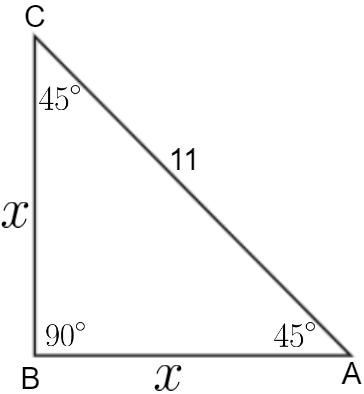
Now, we know that according to the Pythagoras theorem:
\[ \Rightarrow {\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Base}}} \right)^2} + {\left( {{\text{Height}}} \right)^2}\]
Putting all the values from the figure in this formula, we’ll get:
\[ \Rightarrow {\left( {11} \right)^2} = {\left( x \right)^2} + {\left( x \right)^2}\]
Simplifying it further, we’ll get:
$
   \Rightarrow {x^2} + {x^2} = 121 \\
   \Rightarrow 2{x^2} = 121 \\
   \Rightarrow {x^2} = \dfrac{{121}}{2}
 $
Taking square root both sides, this will give us:
\[
   \Rightarrow x = \sqrt {\dfrac{{121}}{2}} = \dfrac{{11}}{{\sqrt 2 }} \\
   \Rightarrow x = \dfrac{{11\sqrt 2 }}{2}
 \]
Taking its approximate decimal value, this will be:
$
   \Rightarrow x = \dfrac{{11 \times 1.414}}{2} = \dfrac{{15.554}}{2} \\
   \Rightarrow x = 7.77
 $

Thus the lengths of both base and height of the triangle is \[\dfrac{{11\sqrt 2 }}{2}\] or 7.77 units.

Note: (1) If two angles of a triangle are equal then it is called isosceles triangle and if the third angle measures ${90^ \circ }$ then the triangle is called isosceles right angled triangle.
(2) If one of the angles of a triangle measures more than ${90^ \circ }$ then the triangle is called an obtuse angled triangle.
(3) And if all of the angles of a triangle measure less than ${90^ \circ }$ then the triangle is called an acute angled triangle.